题目内容
已知函数f(x)=a|x+b|(a>0,a≠1,b∈R).
(1)若f(x)为偶函数,求b的值;
(2)若f(x)在区间[2,+∞)上是增函数,试求a、b应满足的条件.
(1)若f(x)为偶函数,求b的值;
(2)若f(x)在区间[2,+∞)上是增函数,试求a、b应满足的条件.
考点:函数奇偶性的判断,函数单调性的判断与证明
专题:函数的性质及应用
分析:(1)因为f(x)为偶函数,得到对任意的∈R,都有f(-x)=f(x),求出b;
(2)记h(x)=|x+b|=
,讨论a值得到b的范围.
(2)记h(x)=|x+b|=
|
解答:
解:(1)因为f(x)为偶函数,∴对任意的∈R,都有f(-x)=f(x),
即a|x+b|=a|-x+b|,所以|x+b|=|-x+b|
得 b=0.
(2)记h(x)=|x+b|=
,
①当a>1时,f(x)在区间[2,+∞)上是增函数,即h(x)在区间[2,+∞)上是增函数,
∴-b≤2,b≥-2
②当0<a<1时,f(x)在区间[2,+∞)上是增函数,即h(x)在区间[2,+∞)上是减函数但h(x)在区间[-b,+∞)上是增函数,故不可能
∴f(x)在区间[2,+∞)上是增函数时,a、b应满足的条件为a>1且b≥-2
即a|x+b|=a|-x+b|,所以|x+b|=|-x+b|
得 b=0.
(2)记h(x)=|x+b|=
|
①当a>1时,f(x)在区间[2,+∞)上是增函数,即h(x)在区间[2,+∞)上是增函数,
∴-b≤2,b≥-2
②当0<a<1时,f(x)在区间[2,+∞)上是增函数,即h(x)在区间[2,+∞)上是减函数但h(x)在区间[-b,+∞)上是增函数,故不可能
∴f(x)在区间[2,+∞)上是增函数时,a、b应满足的条件为a>1且b≥-2
点评:本题考查了函数奇偶性的运用以及讨论思想的运用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
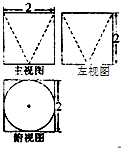
设如图是某几何体的三视图,则该几何体的体积为( )

A、
| ||
B、8-
| ||
| C、8-2π | ||
D、8-
|
为了得到函数y=cos(2x+
)的图象,只需把函数y=sin(2x+
)的函数( )
| π |
| 6 |
| π |
| 6 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
设平面向量
=(-1,0),
=(0,2),则2
+3
等于( )
| a |
| b |
| a |
| b |
| A、(6,3) |
| B、(-2,6) |
| C、(2,1) |
| D、(7,2) |
下面四个选项大小关系正确的是( )
A、sin
| ||||
B、sin
| ||||
C、cos
| ||||
D、cos
|
在△abc 中,∠a:∠b:∠c=1:2:3,那么三边之比 a:b:c 等于( )
| A、1:2:3 | ||
| B、3:2:1 | ||
C、1:
| ||
D、2:
|
