题目内容
已知数列{an}是非常数列的等差数列,Sn为其前n项和,S5=25,且a1,a3,a13成等比数列;数列{bn}满足2log2bn=an+1(n∈N*),{bn}的前n项和为Tn.
(I)求数列{an}、{bn}的通项公式;
(Ⅱ){bn}的前n项和为Tn,求使Tn>2014成立的最小正整数n.
(I)求数列{an}、{bn}的通项公式;
(Ⅱ){bn}的前n项和为Tn,求使Tn>2014成立的最小正整数n.
考点:数列的求和
专题:等差数列与等比数列
分析:(I)设等差数列{an}的公差为d≠0,S5=25,可得
=25=5a3,a3=5,由于a1,a3,a13成等比数列,可得
=a1•a13,
=(a3-2d)•(a3+10d),解得d.利用等差数列的通项公式可得an.由于2log2bn=an+1,可得2log2bn=2n-1+1,解出bn.
(II)利用等比数列的前n项和公式可得Tn.Tn>2014即2n+1-2>2014,即可得出.
| 5(a1+a5) |
| 2 |
| a | 3 3 |
| a | 2 3 |
(II)利用等比数列的前n项和公式可得Tn.Tn>2014即2n+1-2>2014,即可得出.
解答:
解:(I)设等差数列{an}的公差为d≠0,S5=25,
∴
=25=5a3,a3=5,
∵a1,a3,a13成等比数列,
∴
=a1•a13,
∴
=(a3-2d)•(a3+10d),
∴52=(5-2d)(5+10d),d≠0,解得d=2.
∴an=a3+(n-3)d=5+2(n-3)=2n-1.
∵2log2bn=an+1,
∴2log2bn=2n-1+1,
∴bn=2n.
(II){bn}的前n项和为Tn=
=2n+1-2.
Tn>2014即2n+1-2>2014,化为2n>1013,∴n≥10.
∴使Tn>2014成立的最小正整数n=10.
∴
| 5(a1+a5) |
| 2 |
∵a1,a3,a13成等比数列,
∴
| a | 3 3 |
∴
| a | 2 3 |
∴52=(5-2d)(5+10d),d≠0,解得d=2.
∴an=a3+(n-3)d=5+2(n-3)=2n-1.
∵2log2bn=an+1,
∴2log2bn=2n-1+1,
∴bn=2n.
(II){bn}的前n项和为Tn=
| 2(2n-1) |
| 2-1 |
Tn>2014即2n+1-2>2014,化为2n>1013,∴n≥10.
∴使Tn>2014成立的最小正整数n=10.
点评:本题考查了等差数列与等比数列的通项公式性质及其前n项和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
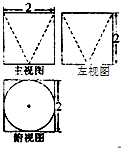
设如图是某几何体的三视图,则该几何体的体积为( )

A、
| ||
B、8-
| ||
| C、8-2π | ||
D、8-
|
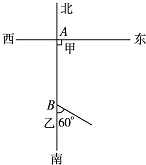 如图,A,B 两个小岛相距21海里,B 岛在 A 岛的正南方,现在甲船从 A 岛出发,以9海里/时的速度向 B 岛行驶,而乙船同时以6海里/时的速度离开 B 岛向南偏东60°方向行驶,行驶多少时间后,两船相距最近?并求出两船的最近距离.
如图,A,B 两个小岛相距21海里,B 岛在 A 岛的正南方,现在甲船从 A 岛出发,以9海里/时的速度向 B 岛行驶,而乙船同时以6海里/时的速度离开 B 岛向南偏东60°方向行驶,行驶多少时间后,两船相距最近?并求出两船的最近距离.