题目内容
设函数f(x)=ex+e-x
(1)判断函数f(x)的奇偶性;
(2)证明函数f(x)在(0,+∞)上是单调增函数.
(1)判断函数f(x)的奇偶性;
(2)证明函数f(x)在(0,+∞)上是单调增函数.
考点:函数奇偶性的判断,函数单调性的判断与证明
专题:函数的性质及应用
分析:(1)利用奇偶性的定义,判断f(-x)与f(x)的关系;
(2)设0<x1<x2,判断f(x1)-f(x2)与0的关系,得到f(x1)与f(x2)大小,根据单调性的定义证明.
(2)设0<x1<x2,判断f(x1)-f(x2)与0的关系,得到f(x1)与f(x2)大小,根据单调性的定义证明.
解答:
(1)解:∵f(x)的定义域为R
∵f(-x)=e-x+ex=f(x)(3分)
∴f(x)为偶函数 (5分)
(2)证明:设0<x1<x2,
f(x1)-f(x2)=ex1+e-x1-ex2-e-x2=ex1-ex2+
-
═(ex1-ex2)(1-
),
因为ex1-ex2<0,
当x>0时,ex>1
∴ex1>1,ex2>1(11分)
∴ex1ex2>1,
<1
1-
>0(12分)
∴f(x1)-f(x2)<0(13分)
∴f(x)在(0,+∞)上单调增函数.(14分)
∵f(-x)=e-x+ex=f(x)(3分)
∴f(x)为偶函数 (5分)
(2)证明:设0<x1<x2,
f(x1)-f(x2)=ex1+e-x1-ex2-e-x2=ex1-ex2+
| 1 |
| ex1 |
| 1 |
| ex2 |
| 1 |
| ex1ex2 |
因为ex1-ex2<0,
当x>0时,ex>1
∴ex1>1,ex2>1(11分)
∴ex1ex2>1,
| 1 |
| ex1ex2 |
1-
| 1 |
| ex1ex2 |
∴f(x1)-f(x2)<0(13分)
∴f(x)在(0,+∞)上单调增函数.(14分)
点评:本题考查了函数的奇偶性和单调性的运用;关键是利用定义解答.

练习册系列答案
相关题目
设如图是某几何体的三视图,则该几何体的体积为( )
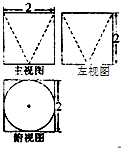

A、
| ||
B、8-
| ||
| C、8-2π | ||
D、8-
|
为了得到函数y=cos(2x+
)的图象,只需把函数y=sin(2x+
)的函数( )
| π |
| 6 |
| π |
| 6 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
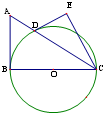 选修4-1:几何证明选讲
选修4-1:几何证明选讲