题目内容
已知函数f(x)=ax2+bx,g(x)=lnx.
(1)当a=1,b=2时,求函数y=f (x)-g (x)的图象在点(1,f (1))处的切线方程;
(2)若2a=1-b(b>1),讨论函数y=f (x)-g (x)的单调性;
(3)若对任意的b∈[-2,-1],均存在x∈(1,e)使得f (x)<g (x),求实数a的取值范围.
(1)当a=1,b=2时,求函数y=f (x)-g (x)的图象在点(1,f (1))处的切线方程;
(2)若2a=1-b(b>1),讨论函数y=f (x)-g (x)的单调性;
(3)若对任意的b∈[-2,-1],均存在x∈(1,e)使得f (x)<g (x),求实数a的取值范围.
考点:利用导数研究曲线上某点切线方程,利用导数研究函数的单调性
专题:导数的综合应用
分析:(1)求函数的导数,利用导数的几何意义即可求出切线方程;
(2)求出函数的导数,利用函数的单调性和导数之间的关系即可;
(3)根据条件分别求出两个函数的最值进行比较即可.
(2)求出函数的导数,利用函数的单调性和导数之间的关系即可;
(3)根据条件分别求出两个函数的最值进行比较即可.
解答:
(1)解:令F(x)=f(x)-g(x)=ax2+bx-lnx,
则F′(x)=2ax+b-
(1分)
当a=1,b=2时,F'(1)=2a+b-1=3,F(1)=a+b=3(2分)
∴函数y=f (x)-g (x)的图象在点(1,f (1))处的切线方程为y-3=3(x-1),
即3x-y=0(3分)
(2)解:F′(x)=(1-b)x+b-
=
=-
(x>0)(5分)
当
<1,即b>2时,F(x)的增区间为(
,1),减区间为(0,
),(1,+∞)(6分)
当
=1,即b=2时,F(x)在(0,+∞)单调递减(7分)
当
>1,即b<2时,F(x)的增区间为(1,
),减区间为(0,1),(
,+∞)(8分)
(3)解:依题意,?b∈[-2,-1],?x∈(1,e)使得f (x)<g (x)成立
即?b∈[-2,-1],?x∈(1,e),F(x)<0成立(9分)
即?b∈[-2,-1],a<
在(1,e)内有解,a<(
)max(10分)
令G(x)=
,则G′(x)=
(11分)
∵b∈[-2,-1],x∈(1,e),
∴-2x+1≤bx+1≤-x+1<0,-2ln x<0
因此G'(x)<0,∴G(x)在(1,e)内单调递减(12分)
又G(1)=-b,∴G(x)max=-b∈[1,2](13分)
∴a≤1,即实数a的取值范围是(-∞,1].(14分)
则F′(x)=2ax+b-
| 1 |
| x |
当a=1,b=2时,F'(1)=2a+b-1=3,F(1)=a+b=3(2分)
∴函数y=f (x)-g (x)的图象在点(1,f (1))处的切线方程为y-3=3(x-1),
即3x-y=0(3分)
(2)解:F′(x)=(1-b)x+b-
| 1 |
| x |
| (1-b)x2+bx-1 |
| x |
| [(b-1)x-1](x-1) |
| x |
当
| 1 |
| b-1 |
| 1 |
| b-1 |
| 1 |
| b-1 |
当
| 1 |
| b-1 |
当
| 1 |
| b-1 |
| 1 |
| b-1 |
| 1 |
| b-1 |
(3)解:依题意,?b∈[-2,-1],?x∈(1,e)使得f (x)<g (x)成立
即?b∈[-2,-1],?x∈(1,e),F(x)<0成立(9分)
即?b∈[-2,-1],a<
| lnx-bx |
| x2 |
| lnx-bx |
| x2 |
令G(x)=
| lnx-bx |
| x2 |
| bx+1-2lnx |
| x3 |
∵b∈[-2,-1],x∈(1,e),
∴-2x+1≤bx+1≤-x+1<0,-2ln x<0
因此G'(x)<0,∴G(x)在(1,e)内单调递减(12分)
又G(1)=-b,∴G(x)max=-b∈[1,2](13分)
∴a≤1,即实数a的取值范围是(-∞,1].(14分)
点评:本题主要考查导数的综合应用,要求熟练掌握,导数的几何意义,函数单调性最值和导数之间的关系,考查学生的综合应用能力.

练习册系列答案
相关题目
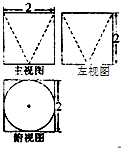
设如图是某几何体的三视图,则该几何体的体积为( )

A、
| ||
B、8-
| ||
| C、8-2π | ||
D、8-
|
为了得到函数y=cos(2x+
)的图象,只需把函数y=sin(2x+
)的函数( )
| π |
| 6 |
| π |
| 6 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
在△abc 中,∠a:∠b:∠c=1:2:3,那么三边之比 a:b:c 等于( )
| A、1:2:3 | ||
| B、3:2:1 | ||
C、1:
| ||
D、2:
|