题目内容
已知函数y=f（x）（x∈R）满足f（x+3）=f（x+1），且x∈[-1，1]时，f（x）=|x|，则函数y=f（x）-log5x（x＞0）的零点个数是 ．
考点：函数零点的判定定理
专题：计算题,作图题,函数的性质及应用
分析：函数y=f（x）-log5x（x＞0）的零点个数可化为函数y=f（x），与函数y=log5x图象的交点个数；作函数图象求解．
解答：
解：由题意，数y=f（x）的周期为2，
函数y=f（x）-log5x（x＞0）的零点个数可化为
函数y=f（x），与函数y=log5x图象的交点个数；
作函数y=f（x）与函数y=log5x的图象如下，
由图象可知，有4个交点，
故函数y=f（x）-log5x（x＞0）的零点个数是4；
故答案为：4．
函数y=f（x）-log5x（x＞0）的零点个数可化为
函数y=f（x），与函数y=log5x图象的交点个数；
作函数y=f（x）与函数y=log5x的图象如下，
由图象可知，有4个交点，
故函数y=f（x）-log5x（x＞0）的零点个数是4；
故答案为：4．
点评：本题考查了函数的零点与函数的图象的关系，同时考查了学生的作图能力，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
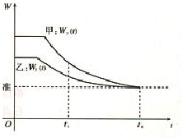国家环保总局对长期超标准排放污物，污染严重而又未进行治理的单位，规定出一定期限，强令在此期限内完成排污治理．如图是国家环保总局在规定的排污达标日期前，对甲、乙两家企业连续检测的结果（W表示排污量），哪个企业治理的效率比较高？为什么？