题目内容
已知函数f(x)当x>0时有意义,并且满足下列条件:
①f(2)=1; ②f(x•y)=f(x)+f(y); ③当x>1时,f(x)>0,
(Ⅰ) 求f(1)、f(
)的值;
(Ⅱ) 证明f(x)在(0,+∞)上是增函数;
(Ⅲ)解不等式f(3)+f(4-8x)>2.
①f(2)=1; ②f(x•y)=f(x)+f(y); ③当x>1时,f(x)>0,
(Ⅰ) 求f(1)、f(
| 1 |
| 2 |
(Ⅱ) 证明f(x)在(0,+∞)上是增函数;
(Ⅲ)解不等式f(3)+f(4-8x)>2.
考点:抽象函数及其应用
专题:函数的性质及应用
分析:(1)在②中令x=y=1,可由f(x•y)=f(x)+f(y),求出f(1)的值;
令x=
,y=2代入②,得f(1)=f(
)+f(2),即0=f(
)+1,从而可求f(
);
(2)在①中令y=
,结合(1)中f(1)=0,当x>1时,f(x)>0,分析f(x2)-f(x1)的符号,结合函数单调性的定义,可得答案.
(3)由f(2)=1,可得2=f(4),结合(2)中函数的单调性,可将不等式转化为不等式组
,解得x的取值范围.
令x=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)在①中令y=
| 1 |
| x |
(3)由f(2)=1,可得2=f(4),结合(2)中函数的单调性,可将不等式转化为不等式组
|
解答:
解:(1)在②中令x=y=1,得f(1)=f(1)+f(1),故 f(1)=0,
令x=
,y=2代入②,得f(1)=f(
)+f(2),即0=f(
)+1,∴f(
)=-1
(2)在②中令y=
,得f(1)=f(x)+f(
),∴0=f(x)+f(
),∴f(x)=-f(
),
函数f(x)在(0,+∞)上的单调递增,理由如下:
任取x1,x2,设x2>x1>0,
∴
>1,
∵当x>1时,f(x)>0,∴f(
)>0
∴f(x2)-f(x1)=f(x2)+f(
)=f(
)>0
f(x2)>f(x1),
∴f(x)在(0,+∞)上是增函数,
(3)由f(2)=1,得2f(2)=2=f(2)+f(2)=f(4),
∴f(3)+f(4-8x)>2可化为f[3×(4-8x)]>f(4),
∴
解得x<
,
不等式的解集为(-∞,
).
令x=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)在②中令y=
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
函数f(x)在(0,+∞)上的单调递增,理由如下:
任取x1,x2,设x2>x1>0,
∴
| x2 |
| x1 |
∵当x>1时,f(x)>0,∴f(
| x2 |
| x1 |
∴f(x2)-f(x1)=f(x2)+f(
| 1 |
| x1 |
| x2 |
| x1 |
f(x2)>f(x1),
∴f(x)在(0,+∞)上是增函数,
(3)由f(2)=1,得2f(2)=2=f(2)+f(2)=f(4),
∴f(3)+f(4-8x)>2可化为f[3×(4-8x)]>f(4),
∴
|
解得x<
| 1 |
| 3 |
不等式的解集为(-∞,
| 1 |
| 3 |
点评:本题考查的知识点是抽象函数及其应用,考查抽象函数值的求法:赋值法,其中熟练掌握抽象函数的解答方法是解答的关键.

练习册系列答案
相关题目
已知集合P={x∈N|1≤x≤10},集合Q={x∈R|x2-x-6=0},则P∩Q等于( )
| A、{2} | B、{1,2} |
| C、{2,3} | D、{3} |
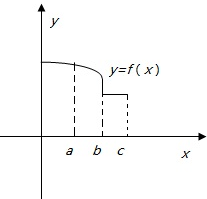 函数y=f(x)的图象如图所示,试画出导函数f′(x)的大致形状.
函数y=f(x)的图象如图所示,试画出导函数f′(x)的大致形状.