题目内容
已知各项均为正数的数列{an}满足an+2+2
=4an+1-an(n∈N*),且a1=1,a2=4.
(Ⅰ)证明:数列{
}是等差数列;
(Ⅱ)设bn=
的前项n和为Sn,求证:Sn<1.
| anan+2 |
(Ⅰ)证明:数列{
| an |
(Ⅱ)设bn=
| 2n+1 |
| anan+1 |
考点:数列递推式,等差关系的确定
专题:等差数列与等比数列
分析:(Ⅰ)通过已知条件,利用配方法推出等差数列的等差中项形式,判断数列是等差数列.
(Ⅱ)求出数列{an}的通项公式,然后利用裂项法求解Sn,即可推出所证明的不等式.
(Ⅱ)求出数列{an}的通项公式,然后利用裂项法求解Sn,即可推出所证明的不等式.
解答:
解:(Ⅰ)∵an+2+2
+an=4an+1且an>0,
∴(
+
)2=(2
)2,
∴
+
=2
,
∴{
}是首项为
=1,公差为
-
=1的等差数列.
(Ⅱ)由(Ⅰ)得
=1+(n-1)×1=n, an=n2,
∴bn=
=
-
,
∴Sn=1-
+
-
+…+
-
=1-
<1.
| anan+2 |
∴(
| an+2 |
| an |
| an+1 |
∴
| an+2 |
| an |
| an+1 |
∴{
| an |
| a1 |
| a2 |
| a1 |
(Ⅱ)由(Ⅰ)得
| an |
∴bn=
| 2n+1 |
| n2(n+1)2 |
| 1 |
| n2 |
| 1 |
| (n+1)2 |
∴Sn=1-
| 1 |
| 22 |
| 1 |
| 22 |
| 1 |
| 32 |
| 1 |
| n2 |
| 1 |
| (n+1)2 |
| 1 |
| (n+1)2 |
点评:本题考查数列的递推关系式的应用,数列的求和以及数列是等差数列的判定,考查计算能力以及转化思想的应用.

练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案
相关题目
用反证法证明命题:“已知a、b∈N*,如果ab可被 5 整除,那么a、b 中至少有一个能被 5 整除”时,假设的内容应为( )
| A、a、b都能被5整除 |
| B、a、b都不能被5整除 |
| C、a、b不都能被5整除 |
| D、a不能被5整除 |
某校新校区建设在市二环路主干道旁,因安全需要,挖掘建设了一条人行地下通道,地下通道设计三视图中的主(正)视力(其中上部分曲线近似为抛物)和侧(左)视图如图(单位:m),则该工程需挖掘的总土方数为( )
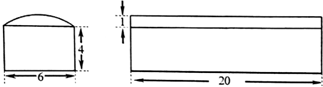

| A、560m3 |
| B、540m3 |
| C、520m3 |
| D、500m3 |
已知i为虚数单位,复数
在复平面内对应的点的坐标为( )
| i |
| i-2 |
A、(
| ||||
B、(-
| ||||
C、(-
| ||||
D、(
|