题目内容
二次函数f(x)=ax2+bx+c中,a>0且a≠1,对于任意的x∈R都有f(x-3)=f(1-x),设m=f(log
),n=f[(
)loga2],则( )
| a |
| 1 |
| a |
| 1 |
| a |
| A、m<n |
| B、m=n |
| C、m>n |
| D、m,n的大小关系不确定 |
考点:不等式比较大小
专题:函数的性质及应用
分析:二次函数f(x)=ax2+bx+c中,a>0且a≠1,对于任意的x∈R都有f(x-3)=f(1-x),可得二次函数f(x)关于直线x=
=-1对称.化简m=f(-2),n=f(
)=f(-
).由于a>0且a≠1,可得函数f(x)在(-∞,-1]上单调递减,即可得出.
| -3+1 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
解答:
解:∵二次函数f(x)=ax2+bx+c中,a>0且a≠1,对于任意的x∈R都有f(x-3)=f(1-x),
∴二次函数f(x)关于直线x=
=-1对称.
∴m=f(log
)=f(-2),
n=f[(
)loga2]=f(
)=f(-
),
∵a>0且a≠1,
∴函数f(x)在(-∞,-1]上单调递减,
∴f(-
)>f(-2).
∴n>m.
故选:A.
∴二次函数f(x)关于直线x=
| -3+1 |
| 2 |
∴m=f(log
| a |
| 1 |
| a |
n=f[(
| 1 |
| a |
| 1 |
| 2 |
| 5 |
| 2 |
∵a>0且a≠1,
∴函数f(x)在(-∞,-1]上单调递减,
∴f(-
| 5 |
| 2 |
∴n>m.
故选:A.
点评:本题考查了二次函数的图象与性质、对数的运算性质,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
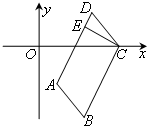 如图,在平行四边形ABCD中,边AD所在直线方程为2x-y-2=0,顶点C(2,0).
如图,在平行四边形ABCD中,边AD所在直线方程为2x-y-2=0,顶点C(2,0).