题目内容
质量m=2kg的物体作直线运动，运动距离s（单位：m）关于时间t（单位：s）的函数是s（t）=3t2+1，且物体的动能U=
mv2，则物体运动后第3s时的动能为（ ）
| 1 |
| 2 |
| A、18焦耳 | B、361焦耳 |
| C、342焦耳 | D、324焦耳 |
考点：变化的快慢与变化率
专题：计算题,导数的概念及应用
分析：先求质点的运动方程为s=3t2+1的导数，再求得t=3秒时的导数，得到所求的瞬时速度，即可求出物体运动后第3s时的动能．
解答：
解：∵质点的运动方程为s=3t2+1
∴s′=6t
∴该质点在t=3秒的瞬时速度为18，
∴物体运动后第3s时的动能为
mv2=324．
故选：D．
∴s′=6t
∴该质点在t=3秒的瞬时速度为18，
∴物体运动后第3s时的动能为
| 1 |
| 2 |
故选：D．
点评：本题考查变化的快慢与变化率，正确解答本题关键是理解导数的物理意义，即了解函数的导数与瞬时速度的关系．
练习册系列答案
相关题目
已知直角三角形的周长为定值2l，则它的面积的最大值为（ ）
A、2
| ||
B、3
| ||
C、（3+2
| ||
D、（3-2
|
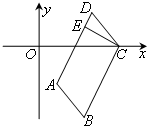如图，在平行四边形ABCD中，边AD所在直线方程为2x-y-2=0，顶点C（2，0）．若?a∈（0，+∞），?θ∈R使asinθ≥a成立，则cos（θ-
）的值为（ ）
| π |
| 6 |
A、
| ||||
B、
| ||||
C、±
| ||||
D、±
|