Question

设实数a＜b，已知函数f（x）=（x-a）²-a，g（x）=（x-b）²-b，令F（x）=

f(x)，f(x)＜g(x) g(x)，f(x)≥g(x)

，若函数y=F（x）+x+a-b有三个零点，则b-a的值是

 

．

Answer 1

考点：根的存在性及根的个数判断

专题：函数的性质及应用

分析：由题意可得y=F（x）的图象和直线y=-x+b-a有3个交点．由f（x）=g（x），求得x=

b+a-1

2

，把x=

b+a-1

2

 代入直线y=-x+b-a，求得点A（

b+a-1

2

，

b-3a+1

2

）．再根据点A在函数f（x）的图象上，可得

b-3a+1

2

=（

b+a-1

2

-a）²-a，由此求得b-a的值．

解答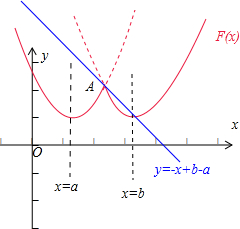： 解：根据函数y=F（x）+x+a-b有三个零点，故y=F（x）的图象和直线y=-x+b-a有3个交点．
由f（x）=g（x），求得x=

b+a-1

2

，故函数f（x）和函数g（x）的图象的交点A的横坐标为

b+a-1

2

，
把x=

b+a-1

2

 代入直线y=-x+b-a可得y=

b-3a+1

2

，故点A（

b+a-1

2

，

b-3a+1

2

）．
再根据点A在函数f（x）的图象上，可得

b-3a+1

2

=（

b+a-1

2

-a）²-a，
化简可得 （b-a）²-4（b-a）-1=0，再结合实数a＜b，可得 b-a=2+

5

，
故答案为：2+

5

．

点评：本题主要考查方程根的存在性以及个数判断，体现了转化、数形结合的数学思想，属于基础题．