题目内容
7.已知函数f(x)=|x|+|x+1|.(1)解关于x的不等式f(x)>3;
(2)若?x∈R,使得m2+3m+2f(x)≥0成立,试求实数m的取值范围.
分析 (1)通过讨论x的范围,得到关于x的不等式组,解出即可;
(2)求出f(x)的最小值,问题转化为m2+3m+2≥0,解出即可.
解答 解:(1)由|x|+|x+1|>3,
得:$\left\{\begin{array}{l}{x≥0}\\{x+x+1>3}\end{array}\right.$或$\left\{\begin{array}{l}{-1<x<0}\\{-x+x+1>3}\end{array}\right.$或$\left\{\begin{array}{l}{x≤-1}\\{-x-x-1>3}\end{array}\right.$,
解得:x>1或x<-2,
故不等式的解集是{x|x>1或x<-2};
(2)若?x∈R,使得m2+3m+2f(x)≥0成立,
而f(x)=$\left\{\begin{array}{l}{2x+1,x≥0}\\{1,-1<x<0}\\{-2x-1,x≤-1}\end{array}\right.$,故f(x)的最小值是1,
故只需m2+3m+2≥0即可,
解得:m≥-1或m≤-2.
点评 本题考查了解绝对值不等式问题,考查绝对值的意义,是一道中档题.

练习册系列答案
相关题目
18.求值:$\frac{1-tan15°}{1+tan15°}$=( )
| A. | $\frac{1}{2}$ | B. | $\sqrt{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\frac{\sqrt{3}}{2}$ |
12.在平面直角坐标系xoy中,双曲线的中心在原点,焦点在y轴上,一条渐近线与直线2x+y-1=0垂直,则双曲线的离心率为( )
| A. | $\frac{{\sqrt{5}}}{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | $\sqrt{5}$ |
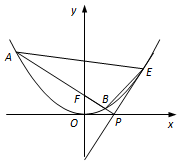 在平面直角坐标系xOy中,已知抛物线x2=2py(p>0)上的点M(m,1)到焦点F的距离为2,
在平面直角坐标系xOy中,已知抛物线x2=2py(p>0)上的点M(m,1)到焦点F的距离为2,