题目内容
11.平面上动点P到点F(0,1)的距离比它到直线l:y=-2的距离小1.(Ⅰ) 求动点P的轨迹C的方程;
(Ⅱ)过点F作直线与曲线C交于两点A,B,与直线l交于点M,求|MA|•|MB|的最小值.
分析 (Ⅰ) 利用平面上动点P到点F(0,1)的距离比它到直线l:y=-2的距离小1,建立方程,即可求动点P的轨迹C的方程;
(Ⅱ)$\overrightarrow{MA}$与$\overrightarrow{MB}$方向相同,故$|MA|•|MB|=|\overrightarrow{MA}•\overrightarrow{MB}|$,直线与抛物线方程联立,利用韦达定理及基本不等式,即可求|MA|•|MB|的最小值.
解答 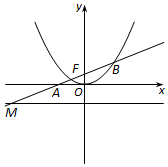 解:(Ⅰ)设动点P的坐标为(x,y),由题意知:$\sqrt{{x^2}+{{(y-1)}^2}}=|y-(-2)|-1=|y+2|-1$,且y≥0,
解:(Ⅰ)设动点P的坐标为(x,y),由题意知:$\sqrt{{x^2}+{{(y-1)}^2}}=|y-(-2)|-1=|y+2|-1$,且y≥0,
∴$\sqrt{{x^2}+{{(y-1)}^2}}=y+1⇒{x^2}+{(y-1)^2}={(y+1)^2}$,化简得:x2=4y,
即为动点P轨迹C的方程; …(4分)
(Ⅱ)设点A(x1,y1),B(x2,y2),M(x0,-2),
由题意直线AB的斜率k
存在且k≠0,设其方程为y=kx+1,则${x_0}=-\frac{3}{k}$,得$M(-\frac{3}{k},-2)$
由$\left\{\begin{array}{l}y=kx+1\\{x^2}=4y\end{array}\right.$,消去y得x2-4kx-4=0,
于是△=16(k2+1)>0恒成立,且x1+x2=4k,x1x2=-4,
又${y_1}{y_2}=(k{x_1}+1)(k{x_2}+1)={k^2}{x_1}{x_2}+k({x_1}+{x_2})+1=1$,${y_1}+{y_2}=k({x_1}+{x_2})+2=4{k^2}+2$…(7分)
∵$\overrightarrow{MA}$与$\overrightarrow{MB}$方向相同,故$|MA|•|MB|=|\overrightarrow{MA}•\overrightarrow{MB}|$,$\overrightarrow{MA}=({x_1}+\frac{3}{k},{y_1}+2),\overrightarrow{MB}=({x_2}+\frac{3}{k},{y_2}+2)$,$\overrightarrow{MA}•\overrightarrow{MB}=({x_1}+\frac{3}{k})({x_2}+\frac{3}{k})+({y_1}+2)({y_2}+2)={x_1}{x_2}+\frac{3}{k}({x_1}+{x_2})+\frac{9}{k^2}+{y_1}{y_2}+2({y_1}+{y_2})+4$
=$8{k^2}+\frac{9}{k^2}+17≥2\sqrt{8{k^2}×\frac{9}{k^2}}+17=17+12\sqrt{2}$,
当且仅当${k^4}=\frac{9}{8}⇒{k^2}=\frac{{3\sqrt{2}}}{4}$时取等号,
故|MA|•|MB|的最小值为$17+12\sqrt{2}$.…(12分)
点评 本题考查抛物线的方程,考查直线与抛物线的位置关系,考查向量知识、韦达定理的运用,属于中档题.

| A. | 294 | B. | 174 | C. | 470 | D. | 304 |