题目内容
6.在平面直角坐标系中,有△ABC,且A(-3,0),B(3,0),顶点C到点A与点B的距离之差为4,则顶点C的轨迹方程为$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{5}$=1(x≥2).分析 利用A(-3,0),B(3,0),顶点C到点A与点B的距离之差为4,由双曲线的定义可得点C的轨迹是焦点在x轴上的双曲线的右支,2a=4,c=3,求出b,即可求出点C的轨迹方程.
解答 解:∵A(-3,0),B(3,0),顶点C到点A与点B的距离之差为4,
∴由双曲线的定义可得点C的轨迹是焦点在x轴上的双曲线的右支,2a=4,c=3,
∴a=2,b=$\sqrt{5}$,
∴点P的轨迹方程为$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{5}$=1(x≥2),
故答案为$\frac{{x}^{2}}{4}-\frac{{y}^{2}}{5}$=1(x≥2).
点评 本题考查点C的轨迹方程,考查双曲线的定义,正确运用双曲线的定义是关键.

练习册系列答案
 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案
相关题目
17.在△ABC中,角A,B,C所对的边分别为a,b,c,已知cosA=$\frac{1}{3}$.求sin(B+C)的值( )
| A. | $\frac{{2\sqrt{2}}}{3}$ | B. | -$\frac{1}{2}$ | C. | 0 | D. | $\frac{3}{4}$ |
15.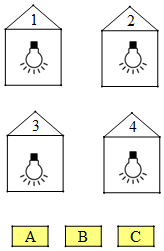 如图,A,B,C三个开关控制着1,2,3,4号四盏灯.若开关A控制着2,3,4号灯(即按一下开关A,2,3,4号灯亮,再按一下开关A,2,3,4号灯熄灭),同样,开关B控制着1,3,4号灯,开关C控制着1,2,4号灯.开始时,四盏灯都亮着,那么下列说法正确的是( )
如图,A,B,C三个开关控制着1,2,3,4号四盏灯.若开关A控制着2,3,4号灯(即按一下开关A,2,3,4号灯亮,再按一下开关A,2,3,4号灯熄灭),同样,开关B控制着1,3,4号灯,开关C控制着1,2,4号灯.开始时,四盏灯都亮着,那么下列说法正确的是( )
 如图,A,B,C三个开关控制着1,2,3,4号四盏灯.若开关A控制着2,3,4号灯(即按一下开关A,2,3,4号灯亮,再按一下开关A,2,3,4号灯熄灭),同样,开关B控制着1,3,4号灯,开关C控制着1,2,4号灯.开始时,四盏灯都亮着,那么下列说法正确的是( )
如图,A,B,C三个开关控制着1,2,3,4号四盏灯.若开关A控制着2,3,4号灯(即按一下开关A,2,3,4号灯亮,再按一下开关A,2,3,4号灯熄灭),同样,开关B控制着1,3,4号灯,开关C控制着1,2,4号灯.开始时,四盏灯都亮着,那么下列说法正确的是( )| A. | 只需要按开关A,C可以将四盏灯全部熄灭 | |
| B. | 只需要按开关B,C可以将四盏灯全部熄灭 | |
| C. | 按开关A,B,C可以将四盏灯全部熄灭 | |
| D. | 按开关A,B,C无法将四盏灯全部熄灭 |
16.已知点P(x,y)的坐标满足x2+y2-2y=0,则$u=\frac{y+1}{x}$的取值范围是( )
| A. | $-\sqrt{3}≤u≤\sqrt{3}$ | B. | $u≥\sqrt{3}$或$u≤-\sqrt{3}$ | C. | $-\frac{{\sqrt{3}}}{3}≤u≤\frac{{\sqrt{3}}}{3}$ | D. | $u≥\frac{{\sqrt{3}}}{3}$或$u≤-\frac{{\sqrt{3}}}{3}$ |
 如图,在公路MN两侧分别有A1,A2,…,A7七个工厂,各工厂与公路MN(图中粗线)之间有小公路连接.现在需要在公路MN上设置一个车站,选择站址的标准是“使各工厂到车站的距离之和越小越好”.则下面结论中正确的是( )
如图,在公路MN两侧分别有A1,A2,…,A7七个工厂,各工厂与公路MN(图中粗线)之间有小公路连接.现在需要在公路MN上设置一个车站,选择站址的标准是“使各工厂到车站的距离之和越小越好”.则下面结论中正确的是( )