题目内容
10．已知向量$\overrightarrow{a}$=（3，1），$\overrightarrow{b}$=（1，3），$\overrightarrow{c}$=（k，-2），若（$\overrightarrow{a}$-$\overrightarrow{c}$）⊥（$\overrightarrow{a}$-$\overrightarrow{b}$），则k=0．分析 根据平面向量的坐标运算与数量积运算，列出方程求出k的值．
解答 解：向量$\overrightarrow{a}$=（3，1），$\overrightarrow{b}$=（1，3），$\overrightarrow{c}$=（k，-2），
则$\overrightarrow{a}$-$\overrightarrow{c}$=（3-k，3），
$\overrightarrow{a}$-$\overrightarrow{b}$=（2，-2），
又（$\overrightarrow{a}$-$\overrightarrow{c}$）⊥（$\overrightarrow{a}$-$\overrightarrow{b}$），
∴（$\overrightarrow{a}$-$\overrightarrow{c}$）⊥（$\overrightarrow{a}$-$\overrightarrow{b}$）=2（3-k）+3×（-2）=0，
解得k=0．
故答案为：0．
点评 本题考查了平面向量的坐标运算与数量积运算问题，是基础题目．
练习册系列答案
相关题目
1．设a∈R，若复数z=$\frac{a-i}{3+i}$（i是虚数单位）的实部为2，则复数z的虚部为（ ）
| A． | 7 | B． | -7 | C． | 1 | D． | -1 |
18．设复数z满足$\frac{z}{|3+4i|}$=$\frac{1-i}{3-4i}$（其中i为虚数单位），则z的共轭复数为（ ）
| A． | $\frac{-7-i}{5}$ | B． | $\frac{-7+i}{5}$ | C． | $\frac{7+i}{5}$ | D． | $\frac{7-i}{5}$ |
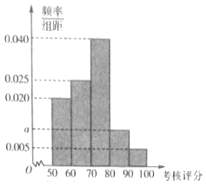2016年，某省环保部门制定了《省工业企业环境保护标准化建设基本要求及考核评分标准》，为了解本省各家企业对环保的重视情况，从中抽取了40家企业进行考核评分，考核评分均在[50，100]内，按照[50，60），[60，70），[70，80），[80，90），[90，100]的分组作出频率分布直方图如图（满分为100分）．