题目内容
18．设复数z满足$\frac{z}{|3+4i|}$=$\frac{1-i}{3-4i}$（其中i为虚数单位），则z的共轭复数为（ ）| A． | $\frac{-7-i}{5}$ | B． | $\frac{-7+i}{5}$ | C． | $\frac{7+i}{5}$ | D． | $\frac{7-i}{5}$ |
分析 利用复数的运算法则、共轭复数的定义、模的计算公式即可得出．
解答 解：∵复数z满足$\frac{z}{|3+4i|}$=$\frac{1-i}{3-4i}$（其中i为虚数单位），
∴z=$\frac{5（1-i）（3+4i）}{（3-4i）（3+4i）}$=$\frac{7+i}{5}$，
则z的共轭复数$\overline{z}$=$\frac{7-i}{5}$．
故选：D．
点评 本题考查了复数的运算法则、共轭复数的定义、模的计算公式，考查了推理能力与计算能力，属于基础题．
练习册系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
在直角坐标系xOy中，设抛物线E：y2=2px（p＞0）的焦点为F，准线为直线l，点A、B在直线l上，点M为抛物线E第一象限上的点，△ABM是边长为$\frac{8}{3}$$\sqrt{3}$的等边三角形，直线MF的倾斜角为60°．
9．
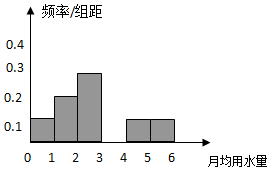某市为了节约生活用水，计划在本市试行居民生活用水定额管理．为了较合理地确定居民日常用水量的标准，有关部门抽样调查了100位居民．表是这100位居民月均用水量（单位：吨）的频率分布表，根据表解答下列问题：
（1）求表中a和b的值；
（2）请将下面的频率分布直方图补充完整，并根据直方图估计该市每位居民月均用水量的众数．
某市为了节约生活用水，计划在本市试行居民生活用水定额管理．为了较合理地确定居民日常用水量的标准，有关部门抽样调查了100位居民．表是这100位居民月均用水量（单位：吨）的频率分布表，根据表解答下列问题：（1）求表中a和b的值；
（2）请将下面的频率分布直方图补充完整，并根据直方图估计该市每位居民月均用水量的众数．
| 分组 | 频数 | 频率 |
| [0，1） | 10 | 0.1 |
| [1，2） | a | 0.2 |
| [2，3） | 30 | 0.3 |
| [3，4） | 20 | b |
| [4，5） | 10 | 0.1 |
| [5，6） | 10 | 0.1 |
| 合计 | 100 | 1 |
10．已知点O为△ABC所在平面内一点，${\overrightarrow{OA}^2}={\overrightarrow{OB}^2}={\overrightarrow{OC}^2}$，若$\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AO}$，且$|{\overrightarrow{AC}}|=|{\overrightarrow{AO}}|$，则$\overrightarrow{AB}$与$\overrightarrow{BC}$的夹角为（ ）
| A． | $\frac{π}{6}$ | B． | $\frac{π}{3}$ | C． | $\frac{2π}{3}$ | D． | $\frac{5π}{6}$ |