题目内容
15.已知函数f(x)=$\left\{\begin{array}{l}{1-{2}^{x},x≤0}\\{{x}^{\frac{1}{2}},x>0}\end{array}\right.$,则f[f(-1)]=$\frac{\sqrt{2}}{2}$.分析 由已知得f(-1)=1-2-1=$\frac{1}{2}$,从而f[f(-1)]=f($\frac{1}{2}$),由此能求出结果.
解答 解:∵函数f(x)=$\left\{\begin{array}{l}{1-{2}^{x},x≤0}\\{{x}^{\frac{1}{2}},x>0}\end{array}\right.$,
f(-1)=1-2-1=$\frac{1}{2}$,
f[f(-1)]=f($\frac{1}{2}$)=$(\frac{1}{2})^{\frac{1}{2}}$=$\frac{\sqrt{2}}{2}$.
故答案为:$\frac{\sqrt{2}}{2}$.
点评 本题考查函数值的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
相关题目
5.已知z=$\frac{i}{1+i}$-$\frac{1}{2i}$(i是虚数单位).那么复数z的虚部为( )
| A. | $\frac{1}{2}$ | B. | i | C. | 1 | D. | -1 |
9.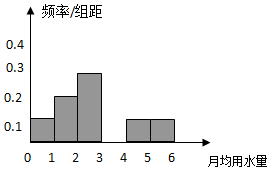 某市为了节约生活用水,计划在本市试行居民生活用水定额管理.为了较合理地确定居民日常用水量的标准,有关部门抽样调查了100位居民.表是这100位居民月均用水量(单位:吨)的频率分布表,根据表解答下列问题:
某市为了节约生活用水,计划在本市试行居民生活用水定额管理.为了较合理地确定居民日常用水量的标准,有关部门抽样调查了100位居民.表是这100位居民月均用水量(单位:吨)的频率分布表,根据表解答下列问题:
(1)求表中a和b的值;
(2)请将下面的频率分布直方图补充完整,并根据直方图估计该市每位居民月均用水量的众数.
 某市为了节约生活用水,计划在本市试行居民生活用水定额管理.为了较合理地确定居民日常用水量的标准,有关部门抽样调查了100位居民.表是这100位居民月均用水量(单位:吨)的频率分布表,根据表解答下列问题:
某市为了节约生活用水,计划在本市试行居民生活用水定额管理.为了较合理地确定居民日常用水量的标准,有关部门抽样调查了100位居民.表是这100位居民月均用水量(单位:吨)的频率分布表,根据表解答下列问题:(1)求表中a和b的值;
(2)请将下面的频率分布直方图补充完整,并根据直方图估计该市每位居民月均用水量的众数.
| 分组 | 频数 | 频率 |
| [0,1) | 10 | 0.1 |
| [1,2) | a | 0.2 |
| [2,3) | 30 | 0.3 |
| [3,4) | 20 | b |
| [4,5) | 10 | 0.1 |
| [5,6) | 10 | 0.1 |
| 合计 | 100 | 1 |
6.若$sinα=\frac{3}{5}(0<α<\frac{π}{2})$,则$sin(α+\frac{π}{6})$=( )
| A. | $\frac{{3\sqrt{3}-4}}{10}$ | B. | $\frac{{3\sqrt{3}+4}}{10}$ | C. | $\frac{{3-4\sqrt{3}}}{10}$ | D. | $\frac{{3+4\sqrt{3}}}{10}$ |
7.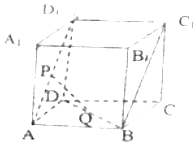 如图,点P、Q分别是正方体ABCD-A1B1C1D1的面对角线AD1、BD的中点,则异面直线PQ和BC1所成的角为( )
如图,点P、Q分别是正方体ABCD-A1B1C1D1的面对角线AD1、BD的中点,则异面直线PQ和BC1所成的角为( )
 如图,点P、Q分别是正方体ABCD-A1B1C1D1的面对角线AD1、BD的中点,则异面直线PQ和BC1所成的角为( )
如图,点P、Q分别是正方体ABCD-A1B1C1D1的面对角线AD1、BD的中点,则异面直线PQ和BC1所成的角为( )| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
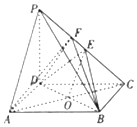 如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为矩形,E为PC的中点,且$PD=AD=\frac{1}{2}AB=4$.
如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD为矩形,E为PC的中点,且$PD=AD=\frac{1}{2}AB=4$.