题目内容
20．函数f（x）=x2在x=1处的切线与两坐标轴围成的三角形的面积为$\frac{1}{4}$．分析 根据求导公式求出函数的导数，把x=1代入求出切线的斜率，求出切点，代入点斜式方程，分别令x=0和y=0求出切线与坐标轴的交点坐标，再代入三角形的面积公式求解．
解答 解：函数f（x）=x2的导数为f′（x）=2x，
可得在x=1处的切线斜率为2，切点为（1，1），
即有在x=1处的切线方程为y-1=2（x-1），
令x=0，可得y=-1；y=0，可得x=$\frac{1}{2}$．
则围成的三角形的面积为$\frac{1}{2}$×1×$\frac{1}{2}$=$\frac{1}{4}$．
故答案为：$\frac{1}{4}$．
点评 本题考查导数的运用：求切线的方程，考查导数的几何意义，以及直线方程的运用，正确求导是解题的关键，属于基础题．
练习册系列答案
举一反三单元同步过关卷系列答案
相关题目
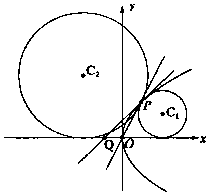如图所示，在直角坐标系xOy中，抛物线C：y2=4x，Q（-1，0），设点P是第一象限内抛物线C上一点，且PQ为抛物线C的切线．
在直角坐标系xOy中，设抛物线E：y2=2px（p＞0）的焦点为F，准线为直线l，点A、B在直线l上，点M为抛物线E第一象限上的点，△ABM是边长为$\frac{8}{3}$$\sqrt{3}$的等边三角形，直线MF的倾斜角为60°．
5．已知z=$\frac{i}{1+i}$-$\frac{1}{2i}$（i是虚数单位）．那么复数z的虚部为（ ）
| A． | $\frac{1}{2}$ | B． | i | C． | 1 | D． | -1 |