在直角坐标系xoy中.曲线C1上的点均在圆C2:(x-5)2+y2=9外.且对C1上任意一点M.M到直线x=-2的距离等于该点与圆C2上点的距离的最小值.则曲线C1的方程为y2=20x．题目和参考答案——青夏教育精英家教网—

题目内容

2．在直角坐标系xoy中，曲线C₁上的点均在圆C₂：（x-5）²+y²=9外，且对C₁上任意一点M，M到直线x=-2的距离等于该点与圆C₂上点的距离的最小值，则曲线C₁的方程为y²=20x．

分析由题设知，曲线C₁上任意一点M到圆心C₂（5，0）的距离等于它到直线x=-5的距离，根据抛物线的定义，可得求曲线C₁的方程．

解答解：由题设知，曲线C₁上任意一点M到圆心C₂（5，0）的距离等于它到直线x=-5的距离，
因此，曲线C₁是以（5，0）为焦点，直线x=-5为准线的抛物线，
故其方程为y²=20x．
故答案为y²=20x．

点评本题考查抛物线的定义，考查学生分析解决问题的能力，正确转化是关键．

练习册系列答案

13．函数$y=\frac{1g（sinx）}{{\sqrt{tanx-1}}}$的定义域为（$\frac{π}{4}$+2kπ，$\frac{π}{2}$+2kπ），k∈Z．

10．已知点O为△ABC所在平面内一点，${\overrightarrow{OA}^2}={\overrightarrow{OB}^2}={\overrightarrow{OC}^2}$，若$\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AO}$，且$|{\overrightarrow{AC}}|=|{\overrightarrow{AO}}|$，则$\overrightarrow{AB}$与$\overrightarrow{BC}$的夹角为（　　）

17．已知函数f（x）=2sin（ωx+φ）+1（ω＞0，|φ|≤$\frac{π}{2}}$），其图象与直线y=2最近的两个相邻交点间的距离为$\frac{π}{3}$，若f（x）＞1对$?x∈（{-\frac{π}{8}，\frac{π}{3}}）$恒成立，则φ的取值范围是（　　）

A．

$[{\frac{π}{4}，\frac{π}{3}}]$

B．

$[{-\frac{π}{6}，\frac{π}{4}}]$

C．

$[{\frac{π}{6}，\frac{π}{4}}]$

D．

$（{\frac{π}{6}，\frac{π}{2}}]$

7．

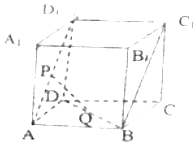如图，点P、Q分别是正方体ABCD-A₁B₁C₁D₁的面对角线AD₁、BD的中点，则异面直线PQ和BC₁所成的角为（　　）

14．过点M（1，1）的直线与双曲线$\frac{x^2}{4}-\frac{y^2}{3}=1$交于A，B两点，且点M平分AB，则直线AB的方程为（　　）

11．

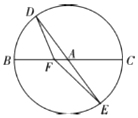如图，BC是单位圆A的一条直径，F是线段AB上的点，且$\overrightarrow{BF}$=3$\overrightarrow{FA}$，若DE是圆A中绕圆心A运动的一条直径，则$\overrightarrow{FD}$•$\overrightarrow{FE}$的值是$-\frac{15}{16}$．

12．已知0＜α＜$\frac{π}{2}$，3sin（π-α）=-2cos（π+α）．
（1）求$\frac{4sinα-2cosα}{5cosα+3sinα}$的值；
（2）求$cos2α+sin（α+\frac{π}{2}）$的值．

试题分类