题目内容
1.在数列{an}中,a1=-2,a2=3,a3=4,an+3+(-1)nan+1=2,记Sn是数列{an}的前n项和,则S40=460.分析 an+3+(-1)nan+1=2,n=2k-1(k∈N*)时,a2k+2-a2k=2,可得数列{an}的偶数项成等差数列,公差为2.n=2k-2(k∈N*)时,a2k+1+a2k-1=2,可得数列{an}的奇数项满足相邻两项的和为2.即可得出.
解答 解:an+3+(-1)nan+1=2,
n=2k-1(k∈N*)时,a2k+2-a2k=2,即数列{an}的偶数项成等差数列,公差为2.
n=2k-2(k∈N*)时,a2k+1+a2k-1=2,即数列{an}的奇数项满足相邻两项的和为2.
∴S40=(a1+a3+…+a39)+(a2+a4+…+a40)
=2×10+$20×3+\frac{20×19}{2}×2$
=460.
故答案为:460.
点评 本题考查了数列递推关系、等差数列的通项公式与求和公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
9.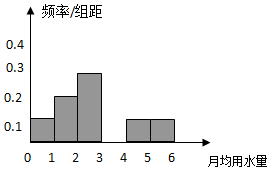 某市为了节约生活用水,计划在本市试行居民生活用水定额管理.为了较合理地确定居民日常用水量的标准,有关部门抽样调查了100位居民.表是这100位居民月均用水量(单位:吨)的频率分布表,根据表解答下列问题:
某市为了节约生活用水,计划在本市试行居民生活用水定额管理.为了较合理地确定居民日常用水量的标准,有关部门抽样调查了100位居民.表是这100位居民月均用水量(单位:吨)的频率分布表,根据表解答下列问题:
(1)求表中a和b的值;
(2)请将下面的频率分布直方图补充完整,并根据直方图估计该市每位居民月均用水量的众数.
 某市为了节约生活用水,计划在本市试行居民生活用水定额管理.为了较合理地确定居民日常用水量的标准,有关部门抽样调查了100位居民.表是这100位居民月均用水量(单位:吨)的频率分布表,根据表解答下列问题:
某市为了节约生活用水,计划在本市试行居民生活用水定额管理.为了较合理地确定居民日常用水量的标准,有关部门抽样调查了100位居民.表是这100位居民月均用水量(单位:吨)的频率分布表,根据表解答下列问题:(1)求表中a和b的值;
(2)请将下面的频率分布直方图补充完整,并根据直方图估计该市每位居民月均用水量的众数.
| 分组 | 频数 | 频率 |
| [0,1) | 10 | 0.1 |
| [1,2) | a | 0.2 |
| [2,3) | 30 | 0.3 |
| [3,4) | 20 | b |
| [4,5) | 10 | 0.1 |
| [5,6) | 10 | 0.1 |
| 合计 | 100 | 1 |
16.某地天气预报说:“明天本地降雨的概率为80%”,这是指( )
| A. | 明天该地区约有80%的时间会下雨,20%的时间不下雨 | |
| B. | 明天该地区约有80%的地方会下雨,20%的地方不下雨 | |
| C. | 明天该地区下雨的可能性为80% | |
| D. | 该地区约有80%的人认为明天会下雨,20%的人认为明天不下雨 |
6.若$sinα=\frac{3}{5}(0<α<\frac{π}{2})$,则$sin(α+\frac{π}{6})$=( )
| A. | $\frac{{3\sqrt{3}-4}}{10}$ | B. | $\frac{{3\sqrt{3}+4}}{10}$ | C. | $\frac{{3-4\sqrt{3}}}{10}$ | D. | $\frac{{3+4\sqrt{3}}}{10}$ |
10.已知点O为△ABC所在平面内一点,${\overrightarrow{OA}^2}={\overrightarrow{OB}^2}={\overrightarrow{OC}^2}$,若$\overrightarrow{AB}+\overrightarrow{AC}=2\overrightarrow{AO}$,且$|{\overrightarrow{AC}}|=|{\overrightarrow{AO}}|$,则$\overrightarrow{AB}$与$\overrightarrow{BC}$的夹角为( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{3}$ | C. | $\frac{2π}{3}$ | D. | $\frac{5π}{6}$ |
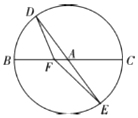 如图,BC是单位圆A的一条直径,F是线段AB上的点,且$\overrightarrow{BF}$=3$\overrightarrow{FA}$,若DE是圆A中绕圆心A运动的一条直径,则$\overrightarrow{FD}$•$\overrightarrow{FE}$的值是$-\frac{15}{16}$.
如图,BC是单位圆A的一条直径,F是线段AB上的点,且$\overrightarrow{BF}$=3$\overrightarrow{FA}$,若DE是圆A中绕圆心A运动的一条直径,则$\overrightarrow{FD}$•$\overrightarrow{FE}$的值是$-\frac{15}{16}$.