题目内容
已知数列{an}的前n项和为Sn,且a1=1,an+1=
Sn,求数列{an}的通项公式.
| 1 |
| 2 |
考点:数列递推式
专题:点列、递归数列与数学归纳法
分析:由数列递推式结合首项求得a2=
,并进一步得到数列{an}从第二项起,是以
为首项,
为公比的等比数列,则数列{an}的通项公式可求.
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
| 2 |
解答:
解:由an+1=
Sn,得
an=
Sn-1(n≥2),
∴an+1-an=
an(n≥2),
即an+1=
an(n≥2),
∵a1=1,
∴a2=
.
∴数列{an}从第二项起,是以
为首项,
为公比的等比数列,
则an=
•(
)n-2(n≥2).
∴an=
.
| 1 |
| 2 |
an=
| 1 |
| 2 |
∴an+1-an=
| 1 |
| 2 |
即an+1=
| 3 |
| 2 |
∵a1=1,
∴a2=
| 1 |
| 2 |
∴数列{an}从第二项起,是以
| 1 |
| 2 |
| 3 |
| 2 |
则an=
| 1 |
| 2 |
| 3 |
| 2 |
∴an=
|
点评:本题考查了数列递推式,考查了等比数列的通项公式,是中档题.

练习册系列答案
相关题目
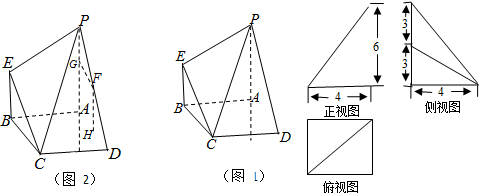
 如图,海上有一座灯塔CD高30米,海面上有两条船A,B,由灯塔
如图,海上有一座灯塔CD高30米,海面上有两条船A,B,由灯塔