Question

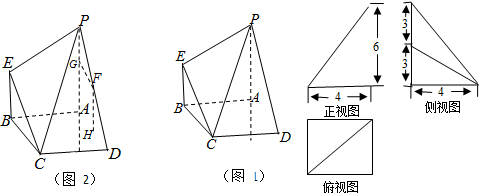
如图1所示是一个几何体的直观图、正视图、俯视图和侧视图（尺寸如图所示，单位cm）；
（Ⅰ）求异面直线CE与PD所成角的正切值；
（Ⅱ）求三棱锥A-EPC的体积；
（Ⅲ）如图2所示F是线段PD上的上的一个动点，过F分别作直线AD、PA的垂线，垂足为H、G，设AH长为x，三棱锥F-PEG与三棱锥F-HCD的体积之和为y，问当x取何值时，y的值最小？并求出该最小值．

Answer 1

考点：异面直线及其所成的角,棱柱、棱锥、棱台的体积

专题：综合题,空间位置关系与距离,空间角

分析：（Ⅰ）取PA中点E₁，证明CE∥DE₁，可得∠PDE₁是异面直线CE与PD所成的角，即可求异面直线CE与PD所成角的正切值；
（Ⅱ）利用V_{三棱锥A-EPC}=V_{三棱锥C-PAE}，求三棱锥A-EPC的体积；
（Ⅲ）由三视图知：VF-PFG=

1

3

(

1

2

•

3

2

x•4)x=x2，VF-HCD=

1

3

[

1

2

•(4-x)•4]

3

2

(4-x)=(4-x)2，可得三棱锥F-PEG与三棱锥F-HCD的体积之和，利用配方法，即可得出结论．

解答： 解：（I）取PA中点E₁，由BE∥AB，AB=BE=3，∴四边形ABEE₁是平行四边形，
∴E₁E∥AB且E₁E=AB，∴E₁E∥CD且E₁E=CD，
∴四边形E₁ECD是平行四边形，
∴CE∥DE₁，∴∠PDE₁是异面直线CE与PD所成的角…（2分）
设∠PDA=α，∠E₁DA=β，则tanα=

3

2

，tanβ=

3

4

，
∴tan∠PDE1=tan(α-β)=

3 2 - 3 4

1+ 9 8

=

6

17

，
∴异面直线CE与PD所成的角的正切值为

6

17

…（4分）
（II）由于三棱锥A-EPC与三棱锥C-PAE是同一几何体，
所以，V_{三棱锥A-EPC}=V_{三棱锥C-PAE}=

1

3

×S△PAE×BC=

1

3

×12×4=16（cm³）…（8分）
（III）依题意得HD=4-x，由

FH

HD

=

6

4

，
∴FH=

3

2

(4-x)，PG=

3

2

x(0＜x＜4)，
由三视图知：VF-PFG=

1

3

(

1

2

•

3

2

x•4)x=x2，VF-HCD=

1

3

[

1

2

•(4-x)•4]

3

2

(4-x)=(4-x)2，
∴y=x²+（4-x）²=2x²-8x+16，x∈（0，4）…（10分）
y=2x²-8x+16=2（x-2）²+8，当x=2时，y_min=8（cm³）…（12分）

点评：本题考查异面直线所成的角，考查三棱锥的体积，考查学生的计算能力，确定三棱锥的体积是关键．