某区有7条南北向街道.5条东西向街道．则从A点走到B点最短的走法有种．题目和参考答案——青夏教育精英家教网—

题目内容

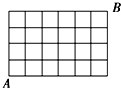某区有7条南北向街道，5条东西向街道（如图）．则从A点走到B点最短的走法有

种．

考点：排列、组合及简单计数问题

专题：应用题,概率与统计

分析：从A到B最短的走法，无论怎样走，一定包括10段，其中6段方向相同，另4段方向相同，每种最短走法，即是从10段中选出6段走东向的，选出4段走北向的，由组合数和计数原理可得．

解答： 解：每条东西向的街道被分成六段，每条南北向的街道被分成4段，
从A到B最短的走法，无论怎样走，一定包括10段，其中6段方向相同，另4段方向相同，
每种最短走法，即是从10段中选出6段走东向的，选出4段走北向的，
故共有

=210种走法．
故答案为：210．

点评：本题考查排列组合的简单应用，得出组成矩形的条件和最短走法是解决问题的关键，属基础题．

练习册系列答案

相关题目

（n∈N^*），a₂=2，S_n是数列{a_n}的前n项和，则S₂₁=

，有下列4个命题：
①任取x₁、x₂∈[0，+∞），都有|f（x₁）-f（x₂）|≤2恒成立；
②f（x）=2kf（x+2k）（k∈N^*），对于一切x∈[0，+∞）恒成立；
③函数y=f（x）-ln（x-1）有3个零点；
④对任意x＞0，不等式f（x）≤

2n+1，	n为奇数
2n，	n为偶数

，则a₄+a₅=

．

△ABC的内角∠A、∠B、∠C的对边分别是a、b、c，若∠B=2∠A，a=1，b=

，则c=

．

已知m，n是直线，α，β，γ是平面，给出下列命题：
①若α⊥γ，β⊥γ，则α∥β；
②若n⊥α，n⊥β，则α∥β；
③若α内不共线的三点到β的距离都相等，则α∥β；
④若n?α，m?α，且n∥β，m∥β，则α∥β；
⑤若m，n为异面直线，n?α，n∥β，m?β，m∥β，则α∥β．
则其中正确的命题是

．（把你认为正确的命题序号都填上）

直线l₁与直线l₂：3x+2y-12=0的交点在x轴上，并且l₁⊥l₂，则l₁在y轴上的截距是（　　）

已知直线a，b，c和平面α，β，γ，下列说法正确的是（　　）

试题分类