题目内容
已知函数f(x)=cosx,则f′(
)等于( )
| π |
| 3 |
A、
| ||||
B、-
| ||||
C、-
| ||||
D、
|
考点:导数的运算
专题:导数的概念及应用
分析:根据求导法则,代入计算即可.
解答:
解:∵f(x)=cosx,
∴f′(x)=-sinx,
∴f′(
)=-sin
=-
故选:C.
∴f′(x)=-sinx,
∴f′(
| π |
| 3 |
| π |
| 3 |
| ||
| 2 |
故选:C.
点评:本题主要考查了初等基本函数的导数,属于基础题.

练习册系列答案
相关题目
已知Sn是等差数列{an} (n∈N*)的前n项和,且S6>S7>S5,有下列四个命题:
①d<0;②S11>0;③S12<0;④数列{Sn}中的最大项为S11.其中正确的命题是( )
①d<0;②S11>0;③S12<0;④数列{Sn}中的最大项为S11.其中正确的命题是( )
| A、①② | B、①③ | C、②③ | D、①④ |
在(
+1)10的展开式中,x4的项的系数是( )
| x |
| A、45 | B、50 | C、55 | D、60 |
| ∫ | 2 1 |
| 1 |
| x |
| A、1 | B、2 | C、ln2 | D、-ln2 |
已知函数f(x)=x3-x2+1,则f(x)在点(1,1)处的切线的倾斜角为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
平面α的一个法向量为(1,2,0),平面β的一个法向量为(2,-1,0),则平面α与平面β的位置关系是( )
| A、平行 | B、相交但不垂直 |
| C、垂直 | D、不能确定 |
用反证法证明命题“自然数a,b,c中三个均为偶数”的反设( )
| A、全是奇数 |
| B、恰有一个偶数 |
| C、至少有一个偶数 |
| D、至多有两个偶数 |
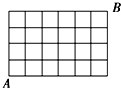 某区有7条南北向街道,5条东西向街道(如图).则从A点走到B点最短的走法有
某区有7条南北向街道,5条东西向街道(如图).则从A点走到B点最短的走法有