题目内容
已知数列{an}满足an=
,则a4+a5= .
|
考点:数列的概念及简单表示法
专题:点列、递归数列与数学归纳法
分析:利用分段数列的意义即可得出.
解答:
解:∵数列{an}满足an=
,∴a1=2×1+1=3,a2=22=4,a3=2×3+1=7,a4=24=16,a5=2×5+1=11.
则a4+a5=16+11=27.
故答案为:27.
|
则a4+a5=16+11=27.
故答案为:27.
点评:本题考查了分段数列的性质,属于基础题.

练习册系列答案
相关题目
已知Sn是等差数列{an} (n∈N*)的前n项和,且S6>S7>S5,有下列四个命题:
①d<0;②S11>0;③S12<0;④数列{Sn}中的最大项为S11.其中正确的命题是( )
①d<0;②S11>0;③S12<0;④数列{Sn}中的最大项为S11.其中正确的命题是( )
| A、①② | B、①③ | C、②③ | D、①④ |
平面α的一个法向量为(1,2,0),平面β的一个法向量为(2,-1,0),则平面α与平面β的位置关系是( )
| A、平行 | B、相交但不垂直 |
| C、垂直 | D、不能确定 |
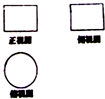 如图所示的是一个立体图形的三视图,此立体图形的名称为:
如图所示的是一个立体图形的三视图,此立体图形的名称为: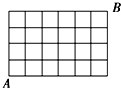 某区有7条南北向街道,5条东西向街道(如图).则从A点走到B点最短的走法有
某区有7条南北向街道,5条东西向街道(如图).则从A点走到B点最短的走法有