题目内容
△ABC的内角∠A、∠B、∠C的对边分别是a、b、c,若∠B=2∠A,a=1,b=
,则c= .
| 3 |
考点:余弦定理
专题:解三角形
分析:由条件利用正弦定理求得cos∠A 的值,可得∠A的值、∠B的值,可得∠C为直角,再利用勾股定理求得c的值.
解答:
解:△ABC中,∵∠B=2∠A,a=1,b=
,故由正弦定理可得
=
,
即
=
,求得cos∠A=
,∴∠A=
,∴∠B=
,∠C=π-∠A-∠B=
.
再利用勾股定理可得 c=
=
=2,
故答案为:2.
| 3 |
| a |
| sin∠A |
| b |
| sin∠B |
即
| 1 |
| sin∠A |
| ||
| sin2∠A |
| ||
| 2 |
| π |
| 6 |
| π |
| 3 |
| π |
| 2 |
再利用勾股定理可得 c=
| a2+b2 |
| 1+3 |
故答案为:2.
点评:本题主要考查正弦定理和余弦定理的应用,属于基础题.

练习册系列答案
相关题目
在(
+1)10的展开式中,x4的项的系数是( )
| x |
| A、45 | B、50 | C、55 | D、60 |
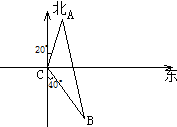 如图,已知两座灯塔A和B与海洋观察站C的距离都等于1km,灯塔A在观察站C的北偏东20°,灯塔B在观察站C的南偏东40°,则灯塔A与灯塔B的距离为( )
如图,已知两座灯塔A和B与海洋观察站C的距离都等于1km,灯塔A在观察站C的北偏东20°,灯塔B在观察站C的南偏东40°,则灯塔A与灯塔B的距离为( )| A、1km | ||
B、
| ||
C、
| ||
| D、2km |
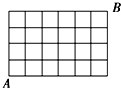 某区有7条南北向街道,5条东西向街道(如图).则从A点走到B点最短的走法有
某区有7条南北向街道,5条东西向街道(如图).则从A点走到B点最短的走法有