题目内容
已知直线a,b,c和平面α,β,γ,下列说法正确的是( )
| A、若a⊥b,b⊥c则a⊥c |
| B、若α⊥β,β⊥γ,则α⊥γ |
| C、若a∥α,b∥β,a∥b,则α∥β |
| D、若α∥β,β∥γ,则α∥γ |
考点:空间中直线与平面之间的位置关系
专题:空间位置关系与距离
分析:根据空间直线和直线,直线和平面之间平行或垂直的判定定理即可得到结论.
解答:
解:A.垂直于同一条直线的两条直线,不一定垂直,故A错误.
B.垂直于同一个平面的两个平面,不一定垂直,可能相交或平行,故B错误.
C.根据面面平行的判定定理可知当直线a,b相交时,结论成立,否则不成立.
D.根据面面平行的性质可知,若α∥β,β∥γ,则α∥γ成立,故D正确,
故选:D.
B.垂直于同一个平面的两个平面,不一定垂直,可能相交或平行,故B错误.
C.根据面面平行的判定定理可知当直线a,b相交时,结论成立,否则不成立.
D.根据面面平行的性质可知,若α∥β,β∥γ,则α∥γ成立,故D正确,
故选:D.
点评:本题主要考查空间直线和平面位置关系的判断,要求熟练掌握相应的判定定理和性质定理.

练习册系列答案
相关题目
已知函数f(x)=x3-x2+1,则f(x)在点(1,1)处的切线的倾斜角为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
平面α的一个法向量为(1,2,0),平面β的一个法向量为(2,-1,0),则平面α与平面β的位置关系是( )
| A、平行 | B、相交但不垂直 |
| C、垂直 | D、不能确定 |
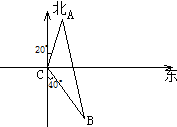 如图,已知两座灯塔A和B与海洋观察站C的距离都等于1km,灯塔A在观察站C的北偏东20°,灯塔B在观察站C的南偏东40°,则灯塔A与灯塔B的距离为( )
如图,已知两座灯塔A和B与海洋观察站C的距离都等于1km,灯塔A在观察站C的北偏东20°,灯塔B在观察站C的南偏东40°,则灯塔A与灯塔B的距离为( )| A、1km | ||
B、
| ||
C、
| ||
| D、2km |
以椭圆C:
+
=1的焦点为顶点,以椭圆C的顶点为焦点的双曲线的方程是( )
| x2 |
| 8 |
| y2 |
| 5 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
“所有9的倍数都是3的倍数.某数是9的倍数,故该数为3的倍数,”上述推理( )
| A、完全正确 |
| B、推理形式不正确 |
| C、错误,因为大小前提不一致 |
| D、错误,因为大前提错误 |
用反证法证明命题“自然数a,b,c中三个均为偶数”的反设( )
| A、全是奇数 |
| B、恰有一个偶数 |
| C、至少有一个偶数 |
| D、至多有两个偶数 |
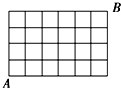 某区有7条南北向街道,5条东西向街道(如图).则从A点走到B点最短的走法有
某区有7条南北向街道,5条东西向街道(如图).则从A点走到B点最短的走法有