题目内容
对于函数f(x)=
,有下列4个命题:
①任取x1、x2∈[0,+∞),都有|f(x1)-f(x2)|≤2恒成立;
②f(x)=2kf(x+2k)(k∈N*),对于一切x∈[0,+∞)恒成立;
③函数y=f(x)-ln(x-1)有3个零点;
④对任意x>0,不等式f(x)≤
恒成立,则实数k的取值范围是[
,+∞).
则其中所有真命题的序号是 .
|
①任取x1、x2∈[0,+∞),都有|f(x1)-f(x2)|≤2恒成立;
②f(x)=2kf(x+2k)(k∈N*),对于一切x∈[0,+∞)恒成立;
③函数y=f(x)-ln(x-1)有3个零点;
④对任意x>0,不等式f(x)≤
| k |
| x |
| 9 |
| 8 |
则其中所有真命题的序号是
考点:分段函数的应用
专题:综合题,数形结合,函数的性质及应用
分析:作出f(x)=
的图象,利用图象可得结论.
|
解答:
 解:f(x)=
解:f(x)=
的图象如图所示:
①f(x)的最大值为1,最小值为-1,∴任取x1、x2∈[0,+∞),都有|f(x1)-f(x2)|≤2恒成立,正确;
②f(
)=2f(
+2)=4f(
+4)=8f(
+6)≠8f(
+8),故不正确;
③如图所示,函数y=f(x)-ln(x-1)有3个零点;
④把(
,
)代入,可得k>
.
故答案为:①③.
 解:f(x)=
解:f(x)=
|
①f(x)的最大值为1,最小值为-1,∴任取x1、x2∈[0,+∞),都有|f(x1)-f(x2)|≤2恒成立,正确;
②f(
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
③如图所示,函数y=f(x)-ln(x-1)有3个零点;
④把(
| 5 |
| 2 |
| 1 |
| 2 |
| 9 |
| 8 |
故答案为:①③.
点评:本题考查分段函数的应用,考查数形结合的数学思想,正确作出函数的图象是关键.

练习册系列答案
 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案
相关题目
已知函数f(x)=x3-x2+1,则f(x)在点(1,1)处的切线的倾斜角为( )
A、
| ||
B、
| ||
C、
| ||
D、
|
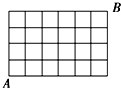 某区有7条南北向街道,5条东西向街道(如图).则从A点走到B点最短的走法有
某区有7条南北向街道,5条东西向街道(如图).则从A点走到B点最短的走法有