题目内容
若关于x的方程
-a+
=0有实数解，求正整数a的取值范围．
| 1+a-x |
| x |
考点：函数的零点
专题：函数的性质及应用
分析：若关于x的方程
-a+
=0有实数解，则关于x的方程
=a-
有实数解，即1+a-x=x+a2-2a
有实数解，即2x-2a
+a2-a-1=0有实数解，即△=（2a）2-8（a2-a-1）≥0，结合a为正整数，可得答案．
| 1+a-x |
| x |
| 1+a-x |
| x |
| x |
| x |
解答：
解：若关于x的方程
-a+
=0有实数解，
则关于x的方程
=a-
有实数解，
即1+a-x=x+a2-2a
有实数解，
即2x-2a
+a2-a-1=0有实数解，
故△=（2a）2-8（a2-a-1）≥0，
即a2-2a-2≤0，
解得：a∈[1-
，1+
]，
又由a为正整数，
故a=1，或a=2
| 1+a-x |
| x |
则关于x的方程
| 1+a-x |
| x |
即1+a-x=x+a2-2a
| x |
即2x-2a
| x |
故△=（2a）2-8（a2-a-1）≥0，
即a2-2a-2≤0，
解得：a∈[1-
| 3 |
| 3 |
又由a为正整数，
故a=1，或a=2
点评：本题考查的知识点是方程的根，其中将问题转化为二次方程根的个数判断，是解答的关键．
练习册系列答案
心算口算巧算一课一练系列答案
应用题作业本系列答案
相关题目
设f（x）是定义在整数集上的函数，且f（x）满足：“当f（k）≥k2成立时，总可以推出f（k+1）≥（k+1）2成立”．那么下列命题总成立的是（ ）
| A、若f（3）≥9成立，则当k≥1时均有f（k）≥k2成立 |
| B、若f（5）≥25成立，则当k≤5时均有f（k）≥k2成立 |
| C、若f（7）＜49成立，则当k≥8时均有f（k）＜k2成立 |
| D、若f（4）=25成立，则当k≥4时均有f（k）≥k2成立 |
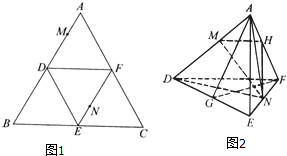如图1，正三角形ABC的边长为2，D、E、F分别为各边的中点将△ABC沿DE、EF、DF折叠，使A、B、C三点重合，构成三棱锥A-DEF如图2．