题目内容
8.设向量$\overrightarrow{a}$=(1,x),$\overrightarrow{b}$=(x,1),若$\overrightarrow{a}$•$\overrightarrow{b}$=-|$\overrightarrow{a}$|•|$\overrightarrow{b}$|,则x=-1.分析 可先求出$\overrightarrow{a}•\overrightarrow{b}=2x$,$|\overrightarrow{a}|=\sqrt{{x}^{2}+1},|\overrightarrow{b}|=\sqrt{{x}^{2}+1}$,然后代入$\overrightarrow{a}•\overrightarrow{b}=-|\overrightarrow{a}||\overrightarrow{b}|$即可得到关于x的方程,解出x即可.
解答 解:$\overrightarrow{a}•\overrightarrow{b}=2x$,$|\overrightarrow{a}|=|\overrightarrow{b}|=\sqrt{{x}^{2}+1}$;
∴由$\overrightarrow{a}•\overrightarrow{b}=-|\overrightarrow{a}||\overrightarrow{b}|$得:2x=-(x2+1);
解得x=-1.
故答案为:-1.
点评 考查向量坐标的数量积运算,根据向量坐标求向量长度的方法.

练习册系列答案
相关题目
3.过双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)的左焦点的直线交双曲线的左支于A、B两点,且|AB|=6,这样的直线可以作2条,则b的取值范围是( )
| A. | (0,2] | B. | (0,2) | C. | (0,$\sqrt{6}$] | D. | (0,$\sqrt{6}$) |
8.设a=2,b=log23,c=log32,则( )
| A. | b>a>c | B. | a>c>b | C. | a>b>c | D. | c>b>a |
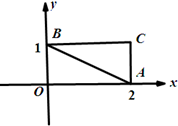 已知椭圆C的方程为$\frac{x^2}{{4{m^2}}}+\frac{y^2}{m^2}$=1,(m>0),如图,△ABC的三个顶点的坐标分别为A(2,0),B(0,1),C(2,1).
已知椭圆C的方程为$\frac{x^2}{{4{m^2}}}+\frac{y^2}{m^2}$=1,(m>0),如图,△ABC的三个顶点的坐标分别为A(2,0),B(0,1),C(2,1).