题目内容

5．如图，梯形ABCD中，AD∥BC，EF是中位线，BD交EF于P，已知EP：PF=1：2，AD=7cm，求BC的长．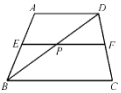

分析 直接利用梯形中位线的性质以及利用三角形中位线的性质与判定得出即可．

解答 解：∵EF是梯形中位线，得EF∥AD∥BC，
∴$\frac{PE}{AD}=\frac{PE}{7}=\frac{BE}{AB}=\frac{1}{2}，\frac{PF}{BC}=\frac{FD}{CD}=\frac{1}{2}$．
∵PE：PF=1：2，
∴BC=2PF=14cm．

点评 此题主要考查了梯形中位线的性质，正确运用梯形中位线的性质以及利用三角形中位线的性质是解题关键．

练习册系列答案
相关题目
7．过抛物线y2=4x的焦点且倾斜角为30°的直线交抛物线于A，B两点，则|AB|=16．
8．设向量$\overrightarrow{a}$=（1，x），$\overrightarrow{b}$=（x，1），若$\overrightarrow{a}$•$\overrightarrow{b}$=-|$\overrightarrow{a}$|•|$\overrightarrow{b}$|，则x=-1．
13．直线2ax+2y-a-1=0与不等式组$\left\{\begin{array}{l}{-x+y-2≤0}\\{x+y-4≤0}\\{x-2y+2≤0}\end{array}\right.$表示的区域没有公共点，则a的取值范围是（　　）
A．（-1，-$\frac{1}{5}$）B．（$\frac{1}{5}$，1）C．（-∞，-1）∪（-$\frac{1}{5}$，+∞）D．（-∞，-5）∪（-1，+∞）
20．如图所示，AB∥CD∥EF，且AO=OD=DF，BC=6，则BE等于（　　）
A．9B．10C．11D．12
10．已知sinα是方程5x2-7x-6=0的根，求：
（1）$\frac{cos（2π-α）cos（π+α）ta{n}^{2}（2π-α）}{cos（\frac{π}{2}+α）sin（2π-α）co{t}^{2}（π-α）}$的值．
（2）在△ABC中，sinA+cosA=$\frac{\sqrt{2}}{2}$，AC=2，AB=3，求tanA的值．
17．函数$f（x）={x^2}+\sqrt{a}x-b+\frac{1}{4}$（a，b是正实数）只有一个零点，则ab的最大值为$\frac{1}{16}$．
14．若集合A={x∈Z|x2+x-12＜0}，B={x|x＜sin5π}，则A∩B中元素的个数为（　　）
A．2B．3C．4D．5
15．数列{an}满足（-1）nan-an-1=2n，n≥2，则{an}的前100项和为（　　）
A．-4750B．4850C．-5000D．4750

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网