题目内容
3.过双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)的左焦点的直线交双曲线的左支于A、B两点,且|AB|=6,这样的直线可以作2条,则b的取值范围是( )| A. | (0,2] | B. | (0,2) | C. | (0,$\sqrt{6}$] | D. | (0,$\sqrt{6}$) |
分析 由双曲线的通径与弦长丨AB丨的关系,即可求得b的取值范围.
解答 解:由题意过双曲线$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{{b}^{2}}$=1(b>0)的左焦点F作直线l与双曲线交于A,B两点,使得|AB|=6,
A,B位于双曲线的左支,即当直线的斜率不存在时,丨AB丨最短,
这样的直线有且仅有两条,则$\frac{{2b}^{2}}{a}$=b2<|AB|=6,
解得0<b<$\sqrt{6}$,
故选D.
点评 本题考查双曲线的弦长与通径的关系,通径公式,属于基础题,

练习册系列答案
相关题目
14.已知sin($\frac{π}{3}$+a)=$\frac{5}{13}$,且a∈($\frac{π}{6}$,$\frac{2π}{3}$),则sin($\frac{π}{12}$+a)的值是( )
| A. | $\frac{17\sqrt{2}}{26}$ | B. | $\frac{-7\sqrt{2}}{26}$ | C. | -$\frac{17\sqrt{2}}{26}$ | D. | $\frac{7\sqrt{2}}{26}$ |
20.如图所示,AB∥CD∥EF,且AO=OD=DF,BC=6,则BE等于( )


| A. | 9 | B. | 10 | C. | 11 | D. | 12 |
1.命题p:“?x0∈R,使得x02-3x0+1≥0”,则命题¬p为( )
| A. | ?x∈R,都有x2-3x+1≤0 | B. | ?x∈R,都有x2-3x+1<0 | ||
| C. | ?x0∈R,使得x02-3x0+1≤0 | D. | ?x0∈R,使得x02-3x0+1<0 |
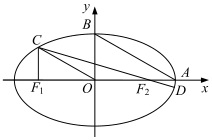 如图,在平面直角坐标系xOy中,设椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,右顶点为A,上顶点为B,离心率为e.椭圆上一点C满足:C在x轴上方,且CF1⊥x轴.
如图,在平面直角坐标系xOy中,设椭圆$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的左、右焦点分别为F1,F2,右顶点为A,上顶点为B,离心率为e.椭圆上一点C满足:C在x轴上方,且CF1⊥x轴.