题目内容
10.若函数f(x)=sin(2x+φ)满足?x∈R,f(x)≤f($\frac{π}{6}$),则f(x)在[0,π]上的单调递增区间为( )| A. | [0,$\frac{π}{6}$]与[$\frac{π}{2}$,$\frac{2π}{3}$] | B. | [$\frac{π}{3}$,$\frac{2π}{3}$] | C. | [0,$\frac{π}{6}$]与[$\frac{2π}{3}$,π] | D. | [0,$\frac{π}{6}$]与[$\frac{π}{3}$,$\frac{2π}{3}$] |
分析 根据题意得出f($\frac{π}{6}$)=1,求出φ的值写出f(x)的解析式;
再求f(x)的单调增区间,即可得出f(x)在x∈[0,π]上的单调增区间.
解答 解:∵f(x)=sin(2x+φ)满足?x∈R,f(x)≤f($\frac{π}{6}$),
∴f($\frac{π}{6}$)=sin(2×$\frac{π}{6}$+φ)=1,
解得φ=$\frac{π}{6}$+2kπ,k∈Z;
∴f(x)=sin(2x+$\frac{π}{6}$);
令-$\frac{π}{2}$+2kπ≤2x+$\frac{π}{6}$≤$\frac{π}{2}$+2kπ,k∈Z,
解得-$\frac{π}{3}$+kπ≤x≤$\frac{π}{6}$+kπ,k∈Z,
当x∈[0,π]时,有[0,$\frac{π}{6}$],[$\frac{2π}{3}$,π]满足条件.
故选:C.
点评 本题考查了正弦函数的图象与性质的应用问题,是基础题目.

练习册系列答案
相关题目
5.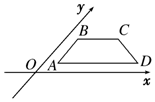 用斜二测画法画出的某平面图形的直观图如图,边AB平行于y轴,BC,AD平行于x轴.已知四边形ABCD的面积为2$\sqrt{2}$ cm2,则原平面图形的面积为( )
用斜二测画法画出的某平面图形的直观图如图,边AB平行于y轴,BC,AD平行于x轴.已知四边形ABCD的面积为2$\sqrt{2}$ cm2,则原平面图形的面积为( )
 用斜二测画法画出的某平面图形的直观图如图,边AB平行于y轴,BC,AD平行于x轴.已知四边形ABCD的面积为2$\sqrt{2}$ cm2,则原平面图形的面积为( )
用斜二测画法画出的某平面图形的直观图如图,边AB平行于y轴,BC,AD平行于x轴.已知四边形ABCD的面积为2$\sqrt{2}$ cm2,则原平面图形的面积为( )| A. | 4 cm2 | B. | 4$\sqrt{2}$ cm2 | C. | 8 cm2 | D. | 8$\sqrt{2}$ cm2 |
15.如果直线 x+2ay-1=0与直线(3a-1)x-ay-1=0平行,则系数a的值为( )
| A. | 0或6 | B. | 0或$\frac{1}{6}$ | C. | 6或 $\frac{1}{6}$ | D. | $\frac{1}{6}$ |
19.《莱因德纸草书》(Rhind Papyrus)是世界上最古老的数学著作之一,书中有这样一道题:把120个面包分成5份,使每份的面包数成等差数列,且较多的三份之和恰好是较少的两份之和的7倍,则最多的那份有面包( )
| A. | 43个 | B. | 45个 | C. | 46个 | D. | 48个 |
20.已知曲线f(x)=x2+a在点(1,f(1))处切线的斜率等于f(2),则实数a值为( )
| A. | -2 | B. | -1 | C. | $\frac{3}{2}$ | D. | 2 |