题目内容
已知数列{an}和{bn}是公比不相等的两个等比数列，cn=an+bn．求证：数列{cn}不是等比数列．
考点：等比数列
专题：等差数列与等比数列
分析：假设{cn}是等比数列，设an=a1•pn-1，bn=b1•qn-1，p≠q，则cn=a1•pn-1+b1•qn-1，由
=
推导出p=q，与题设矛盾，假设错误，故数列{cn}不是等比数列．
| cn+1 |
| cn |
| cn |
| cn-1 |
解答：
证明：用反证法，假设{cn}是等比数列，
设an=a1•pn-1，bn=b1•qn-1，p≠q
则cn=a1•pn-1+b1•qn-1，
∵{cn}是等比数列，∴
=
，①
cn+1=a1•pn+b1•qn，
cn-1=a1•pn-2+b1•qn-2，
代入①并化简可得（p-q）2=0，即p=q
与题设矛盾，假设错误，
∴数列{cn}不是等比数列．
设an=a1•pn-1，bn=b1•qn-1，p≠q
则cn=a1•pn-1+b1•qn-1，
∵{cn}是等比数列，∴
| cn+1 |
| cn |
| cn |
| cn-1 |
cn+1=a1•pn+b1•qn，
cn-1=a1•pn-2+b1•qn-2，
代入①并化简可得（p-q）2=0，即p=q
与题设矛盾，假设错误，
∴数列{cn}不是等比数列．
点评：本题考查数列不是等比数列的证明，是基础题，解题时要认真审题，注意反证法的合理运用．
练习册系列答案
相关题目
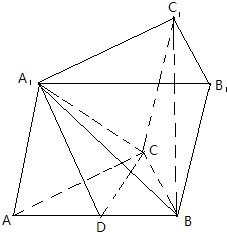如图，在三棱柱ABC-A1B1C1中，AA1⊥BC，∠A1AC=60°，AA1=AC=BC=1，A1B=
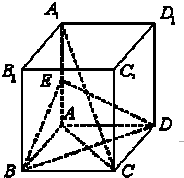如图，在正方体ABCD-A1B1C1D1中，E是AA1的中点．