题目内容
用秦九韶算法求多项式f(x)=1+2x+x2-3x3+2x4,当X=-1时的值,该算法运算次数为 .
考点:秦九韶算法
专题:算法和程序框图
分析:利用秦九韶算法即可得出.
解答:
解:∵f(x)=1+2x+x2-3x3+2x4=(((2x-3)x+1)x+2)x+1,
当X=-1时的值,该算法运算次数为8:其中4次乘法,4次加法.
故答案为:8
当X=-1时的值,该算法运算次数为8:其中4次乘法,4次加法.
故答案为:8
点评:本题考查了秦九韶算法,属于基础题.

练习册系列答案
 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案
相关题目
在2011年3月15日那天,南昌市物价部门对本市的5家商场的某商品的一天销售量及
由散点图可知,销售量y与价格x之间有较好的线性相关关系,根据上表可得回归直线方程是:
=-3.2x+a,则a=( )
| 价格x | 9 | 9.5 | 10 | 10.5 | 11 |
| 销量y | 11 | 10 | 8 | 6 | 5 |
 |
| y |
| A、-24 | B、35.6 |
| C、40.5 | D、40 |
曲线y=
+
在点A(
,1)处的切线斜率为( )
| sinx |
| sinx+cosx |
| 1 |
| 2 |
| π |
| 4 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|

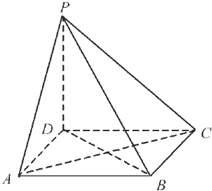 如图,在四棱锥P-ABCD中,底面ABCD是正方形,边长AB=a且PD=a,PA=PC=
如图,在四棱锥P-ABCD中,底面ABCD是正方形,边长AB=a且PD=a,PA=PC=