题目内容
已知函数f(x)=ln(1+ax2),a∈R且a≠0.
(1)当a=-4时,求F(x)=f(x)-2x的最大值;
(2)求f(x)的单调区间;
(3)当n∈N*,求证:
+
+
+…+
>
ln2.
(1)当a=-4时,求F(x)=f(x)-2x的最大值;
(2)求f(x)的单调区间;
(3)当n∈N*,求证:
| 1 |
| 12+n2 |
| 2 |
| 22+n2 |
| 3 |
| 32+n2 |
| n |
| n2+n2 |
| 1 |
| 2 |
考点:利用导数研究函数的单调性,利用导数求闭区间上函数的最值
专题:计算题,证明题,压轴题,导数的综合应用
分析:(1)代入a=-4化简F(x)=ln(1-4x2)-2x的定义域为(-
,
);求导并令F′(x)=
-2=
=0,从而判断导数的正负以确定单调性,再求最大值;
(2)由1+ax2>0知ax2>-1(a≠0),再求导f′(x)=
,讨论a以确定函数的定义域及导数的正负,从而确定函数的单调性;
(3)设不等式左边为Sn,化简Sn=
+
+
+…+
=
[
+
+
+…+
];构造函数g(x)=
,从而化Sn=
[
]=
•g(ξi),其中ξi=
,(i=1,2,3…n);利用积分的定义可知
•g(ξi)表示函数g(x)在区间[0,1]上与x轴围成的面积的过剩近似值;从而证明.
| 1 |
| 2 |
| 1 |
| 2 |
| -8x |
| 1-4x2 |
| 8x2-8x-2 |
| 1-4x2 |
(2)由1+ax2>0知ax2>-1(a≠0),再求导f′(x)=
| 2ax |
| 1+ax2 |
(3)设不等式左边为Sn,化简Sn=
| 1 |
| 12+n2 |
| 2 |
| 22+n2 |
| 3 |
| 32+n2 |
| n |
| n2+n2 |
| 1 |
| n |
| ||
1+(
|
| ||
1+(
|
| ||
1+(
|
| ||
1+(
|
| 2x |
| 1+x2 |
| 1 |
| 2 |
| n |
 |
| i=1 |
| 1 |
| n |
2•
| ||
1+(
|
| 1 |
| 2 |
| n |
 |
| i=1 |
| 1 |
| n |
| i |
| n |
| n |
 |
| i=1 |
| 1 |
| n |
解答:
解:(1)当a=-4时,F(x)=ln(1-4x2)-2x的定义域为(-
,
);
由F′(x)=
-2=
=0,
可得x=
,
∵x∈(-
,
),
∴x=
;
故当x∈(-
,
),F′(x)>0,F(x)单调递增,
当x∈(
,
),F′(x)<0,F(x)单调递减;
故F(x)的最大值为F(
)=ln(2
-2)+
-1.
(2)因为1+ax2>0,可知ax2>-1(a≠0),
又f′(x)=
;
当a>0,f(x)定义域为R,若x>0则f′(x)>0,若x<0则f′(x)<0;
故f(x)的单调减区间为(-∞,0),单调增区间为(0,+∞).
当a<0,f(x)定义域为(-
,
),
若x>0则f′(x)<0,若x<0则f′(x)>0;
故f(x)的单调增区间为(-
,0),单调减区间为(0,
).
(3)证明:设不等式左边为Sn,
则Sn=
+
+
+…+
=
[
+
+
+…+
]
=
[
+
+
+…+
];
构造函数g(x)=
,
由(2)可知当a=1时,f(x)=ln(1+x2),f′(x)=g(x);
Sn=
[
]=
•g(ξi),其中ξi=
,(i=1,2,3…n);
利用积分的定义可知
•g(ξi)表示函数g(x)在区间[0,1]上与x轴围成的面积的过剩近似值;
故有
•g(ξi)>
g(x)dx=
f′(x)dx=[f(1)-f(0)]=ln2;
故当n∈N*,
+
+
+…+
>
ln2成立.
| 1 |
| 2 |
| 1 |
| 2 |
由F′(x)=
| -8x |
| 1-4x2 |
| 8x2-8x-2 |
| 1-4x2 |
可得x=
1±
| ||
| 2 |
∵x∈(-
| 1 |
| 2 |
| 1 |
| 2 |
∴x=
1-
| ||
| 2 |
故当x∈(-
| 1 |
| 2 |
1-
| ||
| 2 |
当x∈(
1-
| ||
| 2 |
| 1 |
| 2 |
故F(x)的最大值为F(
1-
| ||
| 2 |
| 2 |
| 2 |
(2)因为1+ax2>0,可知ax2>-1(a≠0),
又f′(x)=
| 2ax |
| 1+ax2 |
当a>0,f(x)定义域为R,若x>0则f′(x)>0,若x<0则f′(x)<0;
故f(x)的单调减区间为(-∞,0),单调增区间为(0,+∞).
当a<0,f(x)定义域为(-
-
|
-
|
若x>0则f′(x)<0,若x<0则f′(x)>0;
故f(x)的单调增区间为(-
-
|
-
|
(3)证明:设不等式左边为Sn,
则Sn=
| 1 |
| 12+n2 |
| 2 |
| 22+n2 |
| 3 |
| 32+n2 |
| n |
| n2+n2 |
=
| 1 |
| n2 |
| 1 | ||
1+(
|
| 2 | ||
1+(
|
| 3 | ||
1+(
|
| n | ||
1+(
|
=
| 1 |
| n |
| ||
1+(
|
| ||
1+(
|
| ||
1+(
|
| ||
1+(
|
构造函数g(x)=
| 2x |
| 1+x2 |
由(2)可知当a=1时,f(x)=ln(1+x2),f′(x)=g(x);
Sn=
| 1 |
| 2 |
| n |
 |
| i=1 |
| 1 |
| n |
2•
| ||
1+(
|
| 1 |
| 2 |
| n |
 |
| i=1 |
| 1 |
| n |
| i |
| n |
利用积分的定义可知
| n |
 |
| i=1 |
| 1 |
| n |
故有
| n |
 |
| i=1 |
| 1 |
| n |
| ∫ | 1 0 |
| ∫ | 1 0 |
故当n∈N*,
| 1 |
| 12+n2 |
| 2 |
| 22+n2 |
| 3 |
| 32+n2 |
| n |
| n2+n2 |
| 1 |
| 2 |
点评:本题考查利用函数的导数解决函数的最值和单调性问题,并通过构造函数利用微积分的思想证明不等式问题,需要较强的综合运用知识和开拓创新能力.考查了函数的思想、分类讨论思想、数形结合思想、等价转化思想等常用的数学思想.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知双曲线
-
=1的右焦点与抛物线y2=ax的焦点重合,则该抛物线的准线被双曲线所截的线段长度为( )
| x2 |
| 4 |
| y2 |
| 5 |
| A、4 | ||||
| B、5 | ||||
C、
| ||||
D、
|
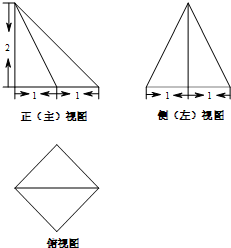 某四棱锥的三视图如图所示,其中正(主)视图是等腰直角三角形,侧(左)视图是等腰三角形,俯视图是正方形,则该四棱锥的体积是( )
某四棱锥的三视图如图所示,其中正(主)视图是等腰直角三角形,侧(左)视图是等腰三角形,俯视图是正方形,则该四棱锥的体积是( )