题目内容
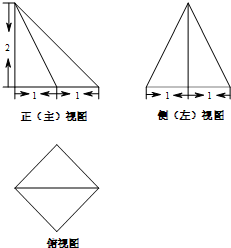 某四棱锥的三视图如图所示,其中正(主)视图是等腰直角三角形,侧(左)视图是等腰三角形,俯视图是正方形,则该四棱锥的体积是( )
某四棱锥的三视图如图所示,其中正(主)视图是等腰直角三角形,侧(左)视图是等腰三角形,俯视图是正方形,则该四棱锥的体积是( )| A、8 | ||
B、
| ||
| C、4 | ||
D、
|
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:由三视图可知,几何体是一个底面是正方形的四棱锥,且一条侧棱垂直于底面.求出底面面积和高,即可求出体积.
解答:
解:由三视图可知,几何体是一个底面是正方形的四棱锥,且一条侧棱垂直于底面.
底面对角线的长为2,底面面积是S=
×22=2,
四棱锥高为h=2,
所以它的体积是
×2×2=
,
故选:D
底面对角线的长为2,底面面积是S=
| 1 |
| 2 |
四棱锥高为h=2,
所以它的体积是
| 1 |
| 3 |
| 4 |
| 3 |
故选:D
点评:本题考查的知识点是由三视图求体积和表面积,解决本题的关键是得到该几何体的形状.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
棱长为2的正方体的外接球的表面积为( )
| A、4π | B、12π |
| C、24π | D、48π |
曲线y=
+1(-2≤x≤2)与直线y=kx-2k+4有两个不同的交点时实数k的范围是( )
| 4-x2 |
A、(
| ||||
B、(
| ||||
C、(
| ||||
D、(-∞,
|
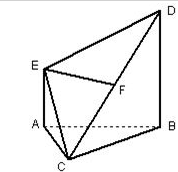 如图,在多面体ABCDE中,AE⊥平面ABC,BD∥AE,△ABC是边长为2的正三角形,且BD=2,AE=1,F为CD中点.
如图,在多面体ABCDE中,AE⊥平面ABC,BD∥AE,△ABC是边长为2的正三角形,且BD=2,AE=1,F为CD中点.