题目内容
9.已知函数f(x)=x2lnx+ax(a∈R)(Ⅰ)求函数f(x)的图象在点(1,f(1))处的切线在y轴上的截距;
(Ⅱ)对于任意的x0>0,记函数f(x)的图象在点(x0,f(x0))处的切线在y轴上的截距为g(x0),求g(x0)的最大值.
分析 (Ⅰ)求出f(x)的导数,求得切线的斜率和切点,运用点斜式方程,可得所求切线的方程,令x=0,即可得到所求y轴上的截距;
(Ⅱ)求出f(x)的导数,可得切线的斜率和切点,由点斜式方程可得切线的方程,可令x=0,可得y轴上的截距,求得g(x0)的导数和单调区间,即可得到所求最大值.
解答 解:(Ⅰ)函数f(x)=x2lnx+ax的导数为f′(x)=2xlnx+x+a,
可得函数f(x)的图象在点(1,f(1))处的切线斜率为1+a,
切点为(1,a),即有切线的方程为y-a=(1+a)(x-1),
令x=0,可得y=a-1-a=-1,
在点(1,f(1))处的切线在y轴上的截距为-1;
(Ⅱ)f(x)的导数为f′(x)=2xlnx+x+a,
可得函数f(x)的图象在点(x0,f(x0))处的切线斜率为2x0lnx0+x0+a,
即有切线的方程为y-(x02lnx0+ax0)=(2x0lnx0+x0+a)(x-x0),
令x=0,可得y=x02lnx0+ax0-x0(2x0lnx0+x0+a)=-x02lnx0-x02,
设g(x0)=-x02lnx0-x02,g′(x0)=-(2x0lnx0+x0)-2x0=-x0(2lnx0+3),
当x0∈(0,e${\;}^{-\frac{3}{2}}$)时,g′(x0)>0,g(x0)递增;
当x0∈(e${\;}^{-\frac{3}{2}}$,+∞)时,g′(x0)<0,g(x0)递减.
可得g(x0)max=g(e${\;}^{-\frac{3}{2}}$)=$\frac{1}{2}$e-3.
点评 本题考查导数的运用:求切线的方程和单调区间、极值和最值,考查直线方程的运用,正确求导是解题的关键,属于中档题.

练习册系列答案
 提分百分百检测卷系列答案
提分百分百检测卷系列答案
相关题目
20.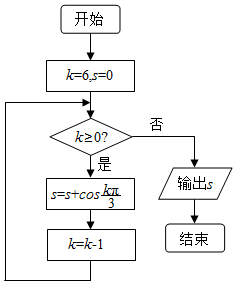 执行如图所示的程序框图,则输出s的值等于( )
执行如图所示的程序框图,则输出s的值等于( )
 执行如图所示的程序框图,则输出s的值等于( )
执行如图所示的程序框图,则输出s的值等于( )| A. | 1 | B. | $\frac{1}{2}$ | C. | 0 | D. | -$\frac{1}{2}$ |
19.各项均不为零的等差数列{an}中,若an+1=an2-an-1(n∈N*,n≥2),则S2016=( )
| A. | 0 | B. | 2 | C. | 2015 | D. | 4032 |





