题目内容
20．
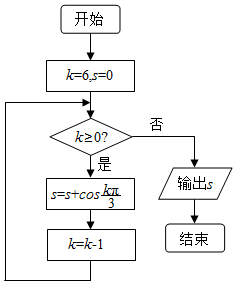执行如图所示的程序框图，则输出s的值等于（ ）| A． | 1 | B． | $\frac{1}{2}$ | C． | 0 | D． | -$\frac{1}{2}$ |
分析 模拟执行如图所示的程序框图，得出该程序输出的是计算S的值，分析最后一次循环过程，即可得出结论．
解答 解：执行如图所示的程序框图，得：
该程序输出的是计算S的值；
当k=0时，满足条件，计算S=cos$\frac{6π}{3}$+cos$\frac{5π}{3}$+cos$\frac{4π}{3}$+cos$\frac{3π}{3}$+cos$\frac{2π}{3}$+cos$\frac{π}{3}$+cos0=1，
当k=-1时，不满足条件，输出S=1．
故选：A．
点评 本题考查了程序框图的应用问题，解题时应模拟程序的运行过程，以便得出正确的答案，是基础题目．
练习册系列答案
相关题目
11．将函数f（x）=sin（x+φ）（|φ|＜$\frac{π}{2}$）的图象向右平移$\frac{π}{6}$个单位后的图象关于y轴对称，则函数f（x）在[0，$\frac{π}{2}$]上的最小值为（ ）
| A． | $\frac{\sqrt{3}}{2}$ | B． | $\frac{1}{2}$ | C． | -$\frac{1}{2}$ | D． | -$\frac{\sqrt{3}}{2}$ |
11．如图程序运行后，得到的a，b，c分别为（ ）
| A． | 2，3，2 | B． | 2，3，1 | C． | 3，2，1 | D． | 3，2，3 |
8．已知F1、F2分别为双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1的左、右焦点，由F1、F2分别作直线l：y=$\frac{2b}{\sqrt{3}a}$（x-1）的垂线段，垂足为M、N，若|MN|=$\sqrt{3}$c，则双曲线的离心率为（ ）
| A． | $\sqrt{3}$ | B． | $\frac{2\sqrt{3}}{3}$ | C． | $\frac{\sqrt{5}}{2}$ | D． | $\frac{\sqrt{10}}{2}$ |
15．
阅读如图所示的程序框图，运行相应的程序．若输入的n=3，则输出的结果为（ ）
阅读如图所示的程序框图，运行相应的程序．若输入的n=3，则输出的结果为（ ）| A． | 6 | B． | 7 | C． | 8 | D． | 9 |
已知函数f（x）=2sin（ωx+φ）（ω＜0，-π＜φ＜π）的部分图象如图所示．