题目内容
1.下列命题中正确的有②③.①常数数列既是等差数列也是等比数列;
②在△ABC中,若sin2A+sin2B=sin2C,则△ABC为直角三角形;
③若A,B为锐角三角形的两个内角,则tanAtanB>1;
④若Sn为数列{an}的前n项和,则此数列的通项an=Sn-Sn-1(n>1).
分析 对4个选项,分别进行判断,即可判断命题的真假.
解答 解:①常数均为0的数列是等差数列,不是等比数列,故不正确;
②在△ABC中,若sin2A+sin2B=sin2C,则a2+b2=c2,所以△ABC为直角三角形,正确;
③因为三角形是锐角三角形,所以A+B>$\frac{π}{2}$即:$\frac{π}{2}$>A>$\frac{π}{2}$-B>0,所以sinA>cosB,同理sinB>cosA,所以tanAtanB=$\frac{sinAsinB}{cosAcosB}$>1,正确;
④若Sn为数列{an}的前n项和,则此数列的通项an=Sn-Sn-1(n>1);n=1,a1=S1,故不正确.
故答案为:②③.
点评 本题考查命题的真假判断,考查等差数列、等比数列的判断,考查正弦定理,数量的通项等基础知识,考查学生分析解决问题的能力,知识综合性强.

练习册系列答案
相关题目
11.如图程序运行后,得到的a,b,c分别为( )


| A. | 2,3,2 | B. | 2,3,1 | C. | 3,2,1 | D. | 3,2,3 |
16.已知函数y=Asin(ωx+φ)(ω>0,-π≤φ<π)的图象如图所示,则φ的值为(
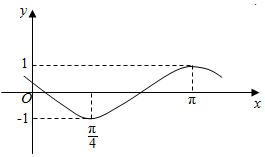

| A. | 0 | B. | -$\frac{5π}{6}$ | C. | $\frac{5π}{6}$ | D. | -$\frac{π}{6}$ |
11.设P为双曲线$\frac{x^2}{a^2}$-y2=1(a>0)的上一点,∠F1PF2=$\frac{2π}{3}$,(F1、F2为左、右焦点),则△F1PF2的面积等于( )
| A. | $\sqrt{3}{a^2}$ | B. | $\frac{{\sqrt{3}}}{3}{a^2}$ | C. | $\frac{{\sqrt{3}}}{3}$ | D. | $\frac{{2\sqrt{3}}}{3}$ |
 已知函数f(x)=2sin(ωx+φ)(ω<0,-π<φ<π)的部分图象如图所示.
已知函数f(x)=2sin(ωx+φ)(ω<0,-π<φ<π)的部分图象如图所示.