题目内容
 一个体积为
一个体积为| 1 |
| 6 |
考点:由三视图求面积、体积
专题:空间位置关系与距离
分析:根据三棱锥的俯视图是一个斜边长为
的等腰直角三角形,可得左视图的宽,再根据体积求得左视图的高,代入三角形的面积公式计算.
| 2 |
解答:
解:由三棱锥的三视图知:底面等腰直角三角形斜边上的高为
,
∴侧视图的宽为
,
设棱锥的高为H,则
×
×
×
×H=
,
∴棱锥的高H=1,
∴侧视图的高为1,又侧视图为直角三角形,
∴侧视图的面积S=
×
×1=
.
故答案为:
.
| ||
| 2 |
∴侧视图的宽为
| ||
| 2 |
设棱锥的高为H,则
| 1 |
| 3 |
| 1 |
| 2 |
| 2 |
| ||
| 2 |
| 1 |
| 6 |
∴棱锥的高H=1,
∴侧视图的高为1,又侧视图为直角三角形,
∴侧视图的面积S=
| 1 |
| 2 |
| ||
| 2 |
| ||
| 4 |
故答案为:
| ||
| 4 |
点评:本题考查了由几何体的体积及正视图、俯视图求侧视图的面积,再三视图中有“长对正,高平齐,宽相等”的规律.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知向量
,
,
满足|
|=4,|
|=2
,
与
的夹角为
,(
-
)•(
-
)=-1,则|
-
|的最大值为( )
| a |
| b |
| c |
| a |
| b |
| 2 |
| a |
| b |
| π |
| 4 |
| c |
| a |
| c |
| b |
| c |
| a |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,已知AB⊥平面ACD,DE⊥平面ACD,AB=2,AC=AD=DE=4,F为CD的中点,
如图,已知AB⊥平面ACD,DE⊥平面ACD,AB=2,AC=AD=DE=4,F为CD的中点,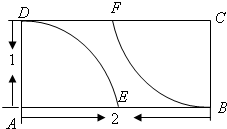 如图,在矩形区域ABCD的A,C两点处各有一个通信基站,假设其信号覆盖范围分别是扇形区域ADE和扇形区域CBF(该矩形区域内无其他信号来源,基站工作正常).若在该矩形区域内随机地选一地点,则该地点无信号的概率是
如图,在矩形区域ABCD的A,C两点处各有一个通信基站,假设其信号覆盖范围分别是扇形区域ADE和扇形区域CBF(该矩形区域内无其他信号来源,基站工作正常).若在该矩形区域内随机地选一地点,则该地点无信号的概率是