题目内容
10.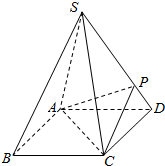 如图,正四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的$\sqrt{2}$倍,CD=$\sqrt{2}$,点P在侧棱SD上,且SP=3PD.
如图,正四棱锥S-ABCD的底面是正方形,每条侧棱的长都是底面边长的$\sqrt{2}$倍,CD=$\sqrt{2}$,点P在侧棱SD上,且SP=3PD.(1)求证:AC⊥SD;
(2)求三棱锥P-ACD的体积.
分析 (1)先证明AC⊥面SBD,然后利用线面垂直的性质证明AC⊥SD;
(2)在OD边上找一点Q,连接PQ,使PQ∥SO.由已知,SO⊥底面ABCD,可得PQ⊥底面ABCD,求出PQ,即可求三棱锥P-ACD的体积.
解答 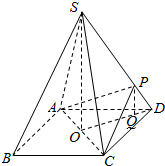 (1)证明:设AC的中点为O,连接OD,OS.
(1)证明:设AC的中点为O,连接OD,OS.
由已知,AC⊥OD,SO⊥底面ABCD,
∵AC?平面ABCD,
∴SO⊥AC,
又∵SO∩DO=O,
∴AC⊥平面SOD,
∵SD?平面SOD,
∴AC⊥SD.…(6分)
(2)解:在OD边上找一点Q,连接PQ,使PQ∥SO.
由已知,SO⊥底面ABCD,
∴PQ⊥底面ABCD,…(8分)
又由已知$CD=\sqrt{2},AC=SC=AS=2$,
则$OS=\sqrt{S{D^2}-O{D^2}}=\sqrt{3}$
∵△SDO∽△PDQ,且SP=3PD,
∴$PQ=\frac{1}{4}SO=\frac{{\sqrt{3}}}{4}$,${S_{△ACD}}=\frac{1}{2}AC•CD=1$,
∴${V_{P-ACD}}=\frac{1}{3}{S_{△ACD}}•PQ=\frac{{\sqrt{3}}}{12}$.…(12分)
点评 本题主要考查线面平行的判定,考查三棱锥P-ACD的体积.要求熟练掌握线面平行的判定定理.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.若角α是三角形的内角,角α的正弦线、余弦线的长度相等,且正弦、余弦符号相异,那么角α=( )
| A. | $\frac{π}{4}$ | B. | $\frac{π}{3}$ | C. | $\frac{3π}{4}$ | D. | $\frac{π}{4}$或$\frac{3π}{4}$ |
5.已知函数f(x)的导函数f′(x),且瞒足f(x)=2xf′(1)+x3,则f′(1)等于( )
| A. | -1 | B. | -3 | C. | 1 | D. | 3 |
5.不等式-x2+3x-2≥0的解集是( )
| A. | {x|x>2或x<1} | B. | {x|x≥2或x≤1} | C. | {x|1≤x≤2} | D. | {x|1<x<2} |
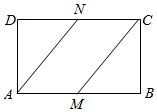 如图在长方形ABCD中,$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AD}=\overrightarrow b,N$是CD的中点,M是线段AB上的点,$|{\overrightarrow a}|=2,|{\overrightarrow b}|=1$.
如图在长方形ABCD中,$\overrightarrow{AB}=\overrightarrow a,\overrightarrow{AD}=\overrightarrow b,N$是CD的中点,M是线段AB上的点,$|{\overrightarrow a}|=2,|{\overrightarrow b}|=1$.