题目内容

5．不等式-x2+3x-2≥0的解集是（　　）
A．{x|x＞2或x＜1}B．{x|x≥2或x≤1}C．{x|1≤x≤2}D．{x|1＜x＜2}

分析 不等式-x2+3x-2≥0化为x2-3x+2≤0，因式分解为（x-1）（x-2）≤0，即可解出．

解答 解：不等式-x2+3x-2≥0化为x2-3x+2≤0，因式分解为（x-1）（x-2）≤0，
解得1≤x≤2．
∴原不等式的解集为{x|1≤x≤2}，
故选：C．

点评 本题考查了基本不等式的性质，考查了推理能力与计算能力，属于中档题．

练习册系列答案
相关题目
19．函数y=$\frac{1}{2}$sinx+$\frac{\sqrt{3}}{2}$cosx（0≤x≤$\frac{π}{2}$）的值域为[$\frac{1}{2}$，1]．
20．化简求值：
（1）sin（x+27°）cos（18°-x）-sin（63°-x）sin（x-18°）
（2）（tan10°-$\sqrt{3}$）•$\frac{cos10°}{sin50°}$．
17．已知函数y=f（x）是定义域为R的奇函数．
（1）证明：f（0）=0；
（2）若y=f（x）在（-∞，+∞）上是增函数，判断y=f（x）在（-∞，0）和（0，+∞）时函数值的正、负符号情况．
4．已知函数f（x）=ln（2x+$\sqrt{4{x}^{2}+1}$）-$\frac{2}{{2}^{x}+1}$，若f（a）=1，则f（-a）=（　　）
A．0B．-1C．-2D．-3
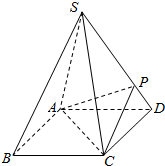10．如图，正四棱锥S-ABCD的底面是正方形，每条侧棱的长都是底面边长的$\sqrt{2}$倍，CD=$\sqrt{2}$，点P在侧棱SD上，且SP=3PD．
（1）求证：AC⊥SD；
（2）求三棱锥P-ACD的体积．
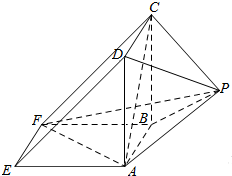17．如图所示，该几何体是由一个直三棱柱ADE-BCF和一个正四棱锥P-ABCD组合而成，AD⊥AF，AE=AD=2．
（Ⅰ）证明：平面PAD⊥平面ABFE；
（Ⅱ）求正四棱锥P-ABCD的高h，使得该四棱锥的体积是三棱锥P-ABF体积的4倍．
14．已知x2+y2-4x-2y-k=0表示图形为圆．
（1）若已知曲线关于直线x+y-4=0的对称圆与直线6x+8y-59=0相切，求实数k的值；
（2）若k=15，求过该曲线与直线x-2y+5=0的交点，且面积最小的圆的方程．
15．已知函数f（x）=sinx-cosx且f′（x）=2f（x），则tanx=（　　）
A．-3B．3C．1D．-1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网