设函数$f(x)=\left\{\begin{array}{l}{2^{-x}}.x＜1\\{log 4}x.x＞1\end{array}\right.$.满足$f(x)=\frac{1}{4}$的x的值是$\sqrt{2}$．题目和参考答案——青夏教育精英家教网—

题目内容

2．设函数$f（x）=\left\{\begin{array}{l}{2^{-x}}，x＜1\\{log_4}x，x＞1\end{array}\right.$，满足$f（x）=\frac{1}{4}$的x的值是$\sqrt{2}$．

分析根据已知中函数$f（x）=\left\{\begin{array}{l}{2^{-x}}，x＜1\\{log_4}x，x＞1\end{array}\right.$，分类讨论满足$f（x）=\frac{1}{4}$的x的值，进而可得答案．

解答解：当x＜1时，解$f（x）={2}^{-x}=\frac{1}{4}$得：x=2（舍去），
当x＞1时，解$f（x）={log}_{4}x=\frac{1}{4}$得：x=$\sqrt{2}$，．
综上，满足$f（x）=\frac{1}{4}$的x的值是$\sqrt{2}$，
故答案为：$\sqrt{2}$

点评本题考查的知识点是分段函数的应用，函数求值，难度中档．

练习册系列答案

17．已知函数y=f（x）是定义域为R的奇函数．
（1）证明：f（0）=0；
（2）若y=f（x）在（-∞，+∞）上是增函数，判断y=f（x）在（-∞，0）和（0，+∞）时函数值的正、负符号情况．

10．

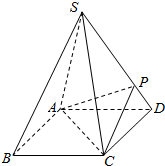如图，正四棱锥S-ABCD的底面是正方形，每条侧棱的长都是底面边长的$\sqrt{2}$倍，CD=$\sqrt{2}$，点P在侧棱SD上，且SP=3PD．
（1）求证：AC⊥SD；
（2）求三棱锥P-ACD的体积．

17．

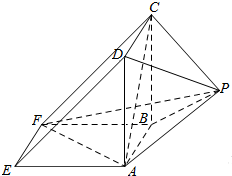如图所示，该几何体是由一个直三棱柱ADE-BCF和一个正四棱锥P-ABCD组合而成，AD⊥AF，AE=AD=2．
（Ⅰ）证明：平面PAD⊥平面ABFE；
（Ⅱ）求正四棱锥P-ABCD的高h，使得该四棱锥的体积是三棱锥P-ABF体积的4倍．

7．（1）在区间[1，5]和[2，4]上分别任取一个整数，记为a，b，则方程$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$表示焦点在x轴上且离心率小于$\frac{{\sqrt{3}}}{2}$的椭圆的概率为多少？
（2）在区间[1，5]和[2，4]上分别任取一个实数，记为a，b，则方程$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$表示焦点在x轴上且离心率小于$\frac{{\sqrt{3}}}{2}$的椭圆的概率为多少？

14．已知x²+y²-4x-2y-k=0表示图形为圆．
（1）若已知曲线关于直线x+y-4=0的对称圆与直线6x+8y-59=0相切，求实数k的值；
（2）若k=15，求过该曲线与直线x-2y+5=0的交点，且面积最小的圆的方程．

11．已知函数f（x）=log₃（2-x）+log₃（x+6）．
（1）求函数f（x）的定义域；
（2）求函数f（x）的最大值．

12．若函数$y={log_2}（{x^2}-ax+3a）$在（2，+∞）上是单调增函数，则实数a的取值范围为（　　）

试题分类