题目内容
已知集合A={a2，a+2}，B={3a-2，2a+1}，若A=B，则实数a的值为（ ）
| A、2 | B、1 | C、-1或1 | D、1或2 |
考点：集合的相等
专题：集合
分析：根据A=B，得到两个集合元素之间的关系，解方程即可求得a值．
解答：
解：∵A={a2，a+2}，B={3a-2，2a+1}，且A=B，
∴若a+2=3a-2，即a=2，此时集合A={4，4}不成立；
若a+2=2a+1，即a=1，此时集合A={1，3}，B={1，3}，满足条件．
∴a=1，
故选：B．
∴若a+2=3a-2，即a=2，此时集合A={4，4}不成立；
若a+2=2a+1，即a=1，此时集合A={1，3}，B={1，3}，满足条件．
∴a=1，
故选：B．
点评：本题主要考查集合相等的应用，根据集合相等得到元素相同是解决本题的关键，注意要进行检验，该题是基础题．
练习册系列答案
各地期末复习特训卷系列答案
小博士期末闯关100分系列答案
相关题目
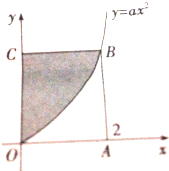如图，长方形的四个顶点为O（0，0），A（2，0），B（2，4），C（0，4）曲线y=ax2经过点B，现将一质点随机投入正方形OABC中，则质点落在图中阴影区域的概率是
如图，已知椭圆C1：