题目内容
已知向量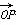 =(cos x,sin x),
=(cos x,sin x), =
=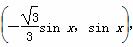 ,定义函数f(x)=
,定义函数f(x)=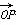 ·
· .
.
(1)求函数f(x)的单调递增区间;
(2)当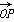 ⊥
⊥ 时,求锐角x的值.
时,求锐角x的值.
解析:(1)由题意知,f(x)=- sin xcos x+sin2x=
sin xcos x+sin2x= -
-
 =
= -
- sin
sin ,f(x)的单调递增区间为sin
,f(x)的单调递增区间为sin 的单调递减区间,即2
的单调递减区间,即2 kπ+
kπ+ ≤2x+
≤2x+ ≤2kπ+
≤2kπ+ (k∈Z),即kπ+
(k∈Z),即kπ+ ≤x≤kπ+
≤x≤kπ+ (k∈Z).故f(x)的单调递增区间为kπ+
(k∈Z).故f(x)的单调递增区间为kπ+ ,kπ+
,kπ+ (k∈Z).
(k∈Z).
(2)当 时,f(x)=0,即
时,f(x)=0,即 -
- sin
sin =0,
=0,
sin =
= ,又x为锐角,所以
,又x为锐角,所以 <2x+
<2x+ <
< ,故2x+
,故2x+ =
= ,故x=
,故x= .
.

练习册系列答案
 培优三好生系列答案
培优三好生系列答案 优化作业上海科技文献出版社系列答案
优化作业上海科技文献出版社系列答案
相关题目

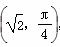 ,圆心为直线ρsin
,圆心为直线ρsin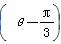 =-
=-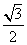 与极轴的交点,求圆C的极坐标方程.
与极轴的交点,求圆C的极坐标方程. =2e1+ke2,
=2e1+ke2, =e1+3e2,
=e1+3e2, =
= 2e1-e2,若A,B,D三点共线,求k的值.
2e1-e2,若A,B,D三点共线,求k的值.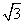 C.2 D.
C.2 D.
 的部分图象如图所示,则
的部分图象如图所示,则 =(
=(  )
)
 C.1 D.2
C.1 D.2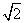 a-c)
a-c) 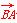 ·
·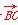 =c
=c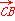 ·
·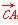 .
.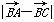 =
=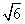 ,求△ABC面积的最大值.
,求△ABC面积的最大值. 9,那么下列不等式中不成立的是( )
9,那么下列不等式中不成立的是( )