题目内容
在△ABC中,角A、B、C的对边分别为a,b,c,且满足(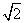 a-c)
a-c) 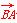 ·
·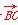 =c
=c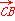 ·
·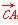 .
.
(1)求角B的大小;
(2)若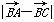 =
=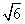 ,求△ABC面积的最大值.
,求△ABC面积的最大值.
解析:(1)(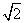 a-c)
a-c) 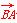 ·
·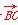 =c
=c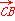 ·
·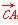 ,
,
可化为:(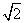 a-c)|
a-c)| 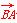 |·|
|·|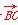 |cos B=c|
|cos B=c|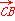 |·|
|·|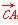 |cos C,
|cos C,
即:(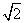 a-c)c
a-c)c acos B=cabcos C,
acos B=cabcos C,
∴(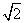 a-c)cos B=bcos C,
a-c)cos B=bcos C,
根据正弦定理有(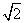 sin A-sin C)cos B=sin Bcos C,
sin A-sin C)cos B=sin Bcos C,
∴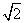 sin Acos B=sin(C+B),即
sin Acos B=sin(C+B),即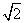 sin Acos B=sin A,
sin Acos B=sin A,
因为sin A>0,所以cos B=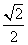 ,即B=
,即B=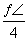 .
.
(2)因为|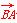 -
-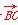 |=
|=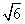 ,所以
,所以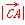 =
=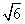 ,即b2=6,
,即b2=6,
根据余弦定理b2=a2+c2-2accos B,
可得6=a2+c2-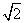 ac,
ac,
由基本不等式可知6=a2+c2-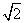 ac≥2ac-
ac≥2ac-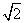 ac=(2-
ac=(2-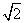 )ac,
)ac,
即ac≤3(2+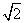 ),
),
故△ABC的面积S=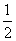 acsin B=
acsin B=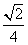 ac≤
ac≤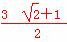 ,
,
即当a=c=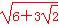 时,
时,
△ABC的面积的最大值为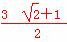 .
.

练习册系列答案
相关题目
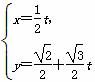 (t为参数),若以直角坐标系xOy的O点为极点,Ox方向为极轴,选择相同的长度单位建立极坐标系,得曲线C的极坐标方程为ρ=2cos
(t为参数),若以直角坐标系xOy的O点为极点,Ox方向为极轴,选择相同的长度单位建立极坐标系,得曲线C的极坐标方程为ρ=2cos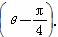 .
. =λ
=λ +μ
+μ ,则λ+μ=________.
,则λ+μ=________.
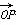 =(cos x,sin x),
=(cos x,sin x), =
=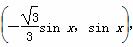 ,定义函数f(x)=
,定义函数f(x)=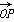 ⊥
⊥ =0,则k=( )
=0,则k=( ) B.
B. C.4 D.0
C.4 D.0 ,若对任意的n∈N*都有an≥a5,则实数b的取值范围是__________.
,若对任意的n∈N*都有an≥a5,则实数b的取值范围是__________.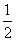 .
.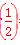 和f
和f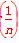 +f
+f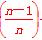 (n∈N)的值;
(n∈N)的值; +…+f
+…+f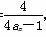 ,Tn=b
,Tn=b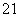 +b
+b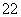 +b
+b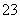 +…+b
+…+b ,Sn=32-
,Sn=32-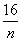 .试比较Tn与Sn的大小.
.试比较Tn与Sn的大小. 列{bn}是首项为a1,公差为d(d≠0)的等差数列,且b1,b3,b11成等比数列.
列{bn}是首项为a1,公差为d(d≠0)的等差数列,且b1,b3,b11成等比数列.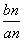 ,求数列{cn}的前n项和Tn.
,求数列{cn}的前n项和Tn.