题目内容
在极坐标系中，已知圆C经过点P
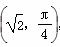，圆心为直线ρsin
＝－
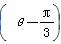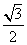与极轴的交点，求圆C的极坐标方程．
解析：在ρsin
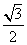＝－中令θ＝0，得ρ＝1，所以圆C的圆心坐标为(1,0)．
因为圆C经过点P
，所以圆C的半径为PC＝
于是圆C过极点，所以圆C的极坐标方程为ρ＝2cos θ.
练习册系列答案
寒假乐园北京教育出版社系列答案
相关题目
寒假乐园北京教育出版社系列答案题目内容
在极坐标系中，已知圆C经过点P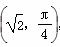，圆心为直线ρsin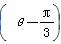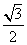＝－与极轴的交点，求圆C的极坐标方程．
解析：在ρsin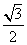＝－中令θ＝0，得ρ＝1，所以圆C的圆心坐标为(1,0)．
因为圆C经过点P，所以圆C的半径为PC＝
于是圆C过极点，所以圆C的极坐标方程为ρ＝2cos θ.
寒假乐园北京教育出版社系列答案
.
的值；
＝－
，求
的值．
，求m的值．
线ρ＝4cos
与直线ρsin
＝1的两个交点之间的距离为________．
(θ为参数)没有公共点，则实数m的取值范围是________________．
(t为参数)，若以直角坐标系xOy的O点为极点，Ox方向为极轴，选择相同的长度单位建立极坐标系，得曲线C的极坐标方程为ρ＝2cos
.
＝(cos x，sin x)，
＝
，定义函数f(x)＝
⊥