题目内容
设点P(x,y)(y≥0)为平面直角坐标系xOy中的一个动点(其中O为坐标原点),点P到定点M(0,
)的距离比点P到x轴的距离大
.
(1)求点P的轨迹方程;
(2)若直线l:y=kx+1与点P的轨迹相交于A、B两点,且|AB|=2
,求k的值.
| 1 |
| 2 |
| 1 |
| 2 |
(1)求点P的轨迹方程;
(2)若直线l:y=kx+1与点P的轨迹相交于A、B两点,且|AB|=2
| 6 |
考点:直线与圆锥曲线的综合问题
专题:圆锥曲线中的最值与范围问题
分析:(1)解法一:过P作x轴的垂线且垂足为N,由题意可知|PM|-|PN|=
,利用两点之间的距离公式即可得出.
解法二:由于点P到定点M(0,
)的距离比点P到x轴的距离大
,可知:点P到定点M(0,
)的距离与P到直线y=-
的距离相等.利用抛物线的定义即可得出.
(2)把y=kx+1与抛物线的方程联立可得关于x的一元二次方程,利用根与系数的关系可得弦长|AB|即可解出k.
| 1 |
| 2 |
解法二:由于点P到定点M(0,
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)把y=kx+1与抛物线的方程联立可得关于x的一元二次方程,利用根与系数的关系可得弦长|AB|即可解出k.
解答:
解:(1)解法一:过P作x轴的垂线且垂足为N,
由题意可知|PM|-|PN|=
,
而y≥0,∴|PN|=y,∴
=y+
.
化简得x2=2y(y≥0)为所求点P的轨迹方程.
解法二:∵点P到定点M(0,
)的距离比点P到x轴的距离大
.
∴点P到定点M(0,
)的距离与P到直线y=-
的距离相等.
可知:点P的轨迹是抛物线,点M为焦点,直线y=-
为准线.
∴x2=-2y.
(2)设A(x1,y1),B(x2,y2),
联立
得x2-2kx-2=0,
∴x1+x2=2k,x1x2=-2.
∴|AB|=
=
=2
,
∴k4+3k2-4=0,而k2≥0,
解得k2=1.
∴k=±1.
由题意可知|PM|-|PN|=
| 1 |
| 2 |
而y≥0,∴|PN|=y,∴
x2+(y-
|
| 1 |
| 2 |
化简得x2=2y(y≥0)为所求点P的轨迹方程.
解法二:∵点P到定点M(0,
| 1 |
| 2 |
| 1 |
| 2 |
∴点P到定点M(0,
| 1 |
| 2 |
| 1 |
| 2 |
可知:点P的轨迹是抛物线,点M为焦点,直线y=-
| 1 |
| 2 |
∴x2=-2y.
(2)设A(x1,y1),B(x2,y2),
联立
|
∴x1+x2=2k,x1x2=-2.
∴|AB|=
| 1+k2 |
| (x1+x2)2-4x1x2 |
| 1+k2 |
| 4k2+8 |
| 6 |
∴k4+3k2-4=0,而k2≥0,
解得k2=1.
∴k=±1.
点评:本题考查了抛物线的定义、直线与抛物线相交问题转化为方程联立可得根与系数的关系、弦长公式、两点之间的距离公式,考查了推理能力与计算能力,属于难题.

练习册系列答案
 寒假天地重庆出版社系列答案
寒假天地重庆出版社系列答案
相关题目
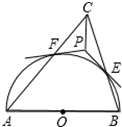 如图,以锐角△ABC的边AB为直径作半圆⊙O交边BC、CA于点E、F.过点E、F分别作⊙O的切线得交点P.求证:CP⊥AB.
如图,以锐角△ABC的边AB为直径作半圆⊙O交边BC、CA于点E、F.过点E、F分别作⊙O的切线得交点P.求证:CP⊥AB. 如图,在正方体OPRS-ABCD中,底面ABCD边长为2,M为OA的中点.
如图,在正方体OPRS-ABCD中,底面ABCD边长为2,M为OA的中点.