题目内容
函数f（x）=2x+2x-6的零点个数为（ ）
| A、0 | B、1 | C、2 | D、3 |
考点：根的存在性及根的个数判断
专题：函数的性质及应用
分析：要判断函数f（x）=2x+2x-6的零点的个数，可以利用图象法，将函数f（x）=2x+2x-6转化为f（x）=2x-（6-2x），然后在同一坐标系中做出函数y=2x，与函数y=-2x+6的图象，分析其交点个数，即可得到答案．
解答：
解：画出函数y=2x，与函数y=-2x+6的图象如图，
由图可知，函数y=2x，与函数y=-2x+6的图象有1个交点，
则函数f（x）=2x+2x-6的零点有1个，
故选B．
解：画出函数y=2x，与函数y=-2x+6的图象如图，由图可知，函数y=2x，与函数y=-2x+6的图象有1个交点，
则函数f（x）=2x+2x-6的零点有1个，
故选B．
点评：本题考查的知识点是函数零点的判定定理，常用的方法有：①零点存在定理②解方程③图象法．当函数的解析式比较复杂，无法解对应的方程时（如本题），多采用图象法．
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
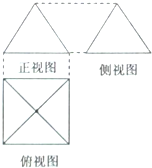如图，一个简单几何体三视图的正视图与侧视图都是边长为2的正三角形，其俯视图轮廓为正方形，则其体积是（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、4
|
函数f（x）=x-a+log2x存在大于1的零点，则a的取值范围是（ ）
| A、[1，∞） |
| B、（1，+∞） |
| C、（0，+∞） |
| D、（-∞，1） |
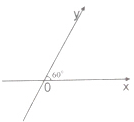如图所示，∠xoy=60°，| e1 |
| e2 |
| m |
| e1 |
| e2 |
| m |
| a |
| a |
| A、1 | ||||
B、
| ||||
C、C
| ||||
D、
|
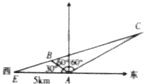如图，某海岛观察哨A测得在海岛北偏东60°的C处有一轮船，80分钟后测得船在海岛北偏西60°的B处，又过20分钟轮船到达位于海岛正西方且距离海岛5km的E港口，如果轮船始终作匀速直线运动，问船速多少？已知函数f（x）=-x2+x，则f（x）从-1到-0.9的平均变化率为（ ）
| A、3 | B、0.29 |
| C、2.09 | D、2.9 |