题目内容
函数f（x）=x-a+log2x存在大于1的零点，则a的取值范围是（ ）
| A、[1，∞） |
| B、（1，+∞） |
| C、（0，+∞） |
| D、（-∞，1） |
考点：函数的零点
专题：函数的性质及应用
分析：由题意可得f（1）＜0，解关于a的不等式可得．
解答：
解：∵函数f（x）=x-a+log2x存在大于1的零点，
∴f（1）=1-a+log21=1-a＜0，
解得a＞1
故选：B
∴f（1）=1-a+log21=1-a＜0，
解得a＞1
故选：B
点评：本题考查函数的零点，属基础题．
练习册系列答案
相关题目
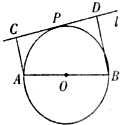如图，设AB为⊙O的任一条不与直线l垂直的直径，P是⊙O与l的公共点，AC⊥l，BD⊥l，垂足分别为C，D，且PC=PD．（Ⅰ）求证：l是⊙O的切线；
（Ⅱ）若⊙O的半径OA=5，AC=4，求CD的长．
函数f（x）=2x+2x-6的零点个数为（ ）
| A、0 | B、1 | C、2 | D、3 |
抛物线y2=px（p＞0）的准线方程为x=-
，则p=（ ）
| 1 |
| 4 |
| A、1 | ||
B、
| ||
C、
| ||
D、
|